In the world of machine learning, evaluating the performance of a model is crucial. This evaluation helps us understand how well our model is predicting or classifying data. Among the many metrics available, Mean Absolute Error (MAE), Mean Squared Error (MSE), and Root Mean Squared Error (RMSE) are three of the most commonly used metrics. But why do we use them? What makes them so important?

1. Mean Absolute Error (MAE)

What is MAE?

Mean Absolute Error measures the average magnitude of errors in a set of predictions, without considering their direction. It’s the average of the absolute differences between predicted values and actual values.

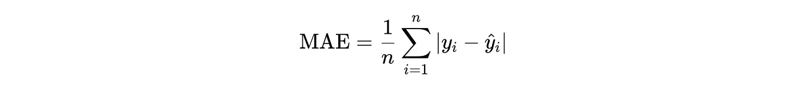
Why use MAE?

• Interpretability: MAE provides a clear, straightforward interpretation of the average error. If MAE is 5, on average, the model’s predictions are 5 units off from the actual values.
• **Robustness: **MAE is less sensitive to outliers compared to MSE and RMSE because it doesn’t square the error terms.

When to use MAE?

MAE is preferred when you want a direct understanding of the average error without exaggerating the impact of large errors. It’s particularly useful when the dataset has outliers or when the cost of errors is linear.

2. Mean Squared Error (MSE)

What is MSE?

Mean Squared Error is the average of the squared differences between the predicted and actual values.

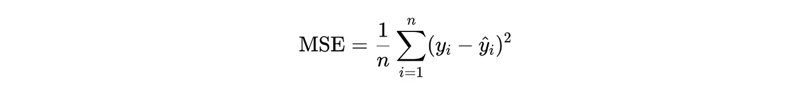
Why use MSE?

• Error Amplification: By squaring the errors, MSE gives more weight to larger errors, making it a good metric when large errors are particularly undesirable.
• Mathematical Properties: MSE is differentiable and often used as a loss function in optimization algorithms like Gradient Descent because its derivative is straightforward to compute. When to use MSE?

MSE is often used when large errors are more problematic than small ones, and when you want the metric to penalize large deviations more heavily. It’s also commonly used during model training, as it’s computationally convenient.

3. Root Mean Squared Error (RMSE)

What is RMSE?

Root Mean Squared Error is the square root of the MSE. It brings the metric back to the original scale of the data, making it easier to interpret than MSE.

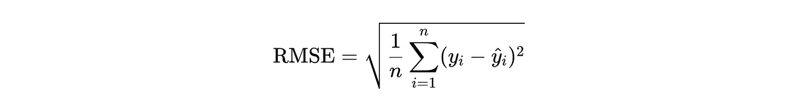
Why use RMSE?

Interpretability on Scale: RMSE, unlike MSE, is on the same scale as the original data, making it more interpretable.
Sensitive to Large Errors: Like MSE, RMSE also penalizes large errors, but since it’s on the original scale, it can provide a more intuitive measure of the error magnitude.

When to use RMSE?

RMSE is preferred when you want a metric that penalizes large errors but still needs the results to be in the same unit as the original data. It’s widely used in contexts where the distribution of error magnitudes matters and where being on the same scale as the data is crucial.

Choosing the Right Metric

• MAE is more robust to outliers and gives an average error in the same unit as the data, making it easy to interpret.
• MSE amplifies larger errors, making it useful when larger errors are particularly costly, and it’s often used as a loss function in model training.
• RMSE combines the benefits of MSE and MAE, offering an error metric that penalizes large errors and remains interpretable.

In practice, the choice between MAE, MSE, and RMSE depends on the specific requirements of the problem at hand. If your application requires a simple, interpretable metric, MAE might be the best choice. If you need to penalize larger errors more severely, MSE or RMSE might be more appropriate.

Graphical representation

1. Setup and Regression Model

Here’s how we can generate a graphical representation of MAE, MSE, and RMSE using a regression model:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error

# Generate some synthetic data for demonstration
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4   3 * X   np.random.randn(100, 1)

# Train a simple linear regression model
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)

# Calculate MAE, MSE, and RMSE
mae = mean_absolute_error(y, y_pred)
mse = mean_squared_error(y, y_pred)
rmse = np.sqrt(mse)

# Plotting the regression line with errors
plt.figure(figsize=(12, 8))

# Scatter plot of actual data points
plt.scatter(X, y, color='blue', label='Actual Data')

# Regression line
plt.plot(X, y_pred, color='red', label='Regression Line')

# Highlighting errors (residuals)
for i in range(len(X)):
    plt.vlines(X[i], y[i], y_pred[i], color='gray', linestyle='dashed')

# Adding annotations for MAE, MSE, RMSE
plt.text(0.5, 8, f'MAE: {mae:.2f}', fontsize=12, bbox=dict(facecolor='white', alpha=0.5))
plt.text(0.5, 7.5, f'MSE: {mse:.2f}', fontsize=12, bbox=dict(facecolor='white', alpha=0.5))
plt.text(0.5, 7, f'RMSE: {rmse:.2f}', fontsize=12, bbox=dict(facecolor='white', alpha=0.5))

# Titles and labels
plt.title('Linear Regression with MAE, MSE, and RMSE')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

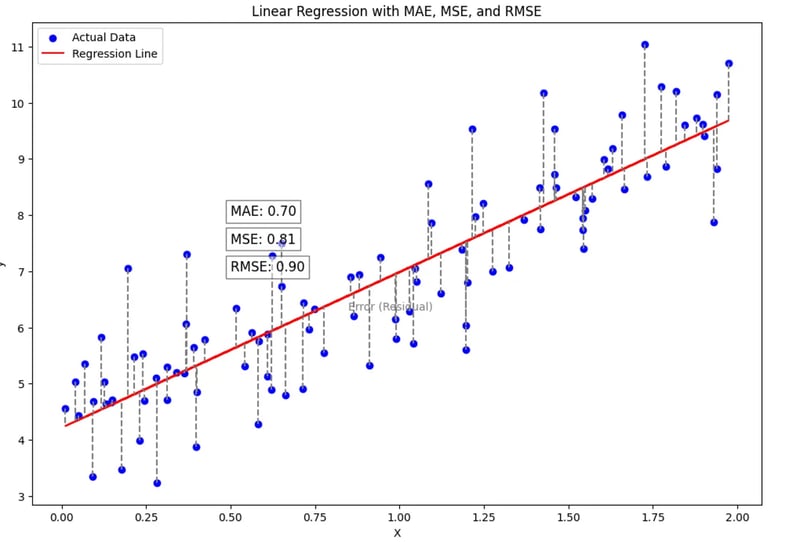
2. Explanation of the Plot

• **Blue Dots: **These represent the actual data points.
• Red Line: This is the regression line that represents the predicted values from the model.
• Gray Lines: These dashed lines represent the residuals or errors for each data point. The length of these lines corresponds to the error magnitude.
• MAE, MSE, RMSE: Annotated in the plot, these values are displayed to help visualize how the model’s performance is evaluated.

3. Interpretation

• MAE: Gives an average error in the same unit as the data, showing the average distance of the data points from the regression line.
• MSE: Squares the errors, emphasizing larger errors more and is often used during the training of regression models.
• RMSE: Provides a metric on the same scale as the original data, making it more interpretable than MSE while still penalizing larger errors.

Training a machine learning model

When training a machine learning model, especially in regression tasks, choosing the right error metric is crucial because it influences how the model learns and how its performance is evaluated. Let’s break down the significance of MAE, MSE, and RMSE in model training:

1. MAE (Mean Absolute Error)

Definition: MAE is the average of the absolute differences between the predicted and actual values.

Significance in Model Training:

• Robustness to Outliers: MAE is less sensitive to outliers compared to MSE and RMSE because it treats all errors equally without squaring them. This means that during training, the model will aim to minimize the average error without disproportionately focusing on larger errors.
• Linear Penalty: The linear nature of MAE means that the impact of each error on the model’s learning process is directly proportional to the magnitude of that error.
• Interpretability: MAE is in the same units as the original data, making it easier to interpret. If the MAE is 5, it means that on average, the model’s predictions are off by 5 units.

2. MSE (Mean Squared Error)

Definition: MSE is the average of the squared differences between the predicted and actual values.

Significance in Model Training:

• Sensitivity to Outliers: MSE is sensitive to outliers because it squares the error, making larger errors much more significant in the calculation. This causes the model to prioritize reducing large errors during training.
• Punishing Large Errors: The squaring effect means that the model will penalize larger errors more severely, which can lead to a better fit for most data points but might overfit to outliers.
• Smooth Gradient: MSE is widely used in optimization algorithms like gradient descent because it provides a smooth gradient, making it easier for the model to converge during training.
• Model’s Focus on Large Errors: Since large errors have a bigger impact, the model might focus on reducing these at the cost of slightly increasing smaller errors, which can be beneficial if large errors are particularly undesirable in the application.

3. RMSE (Root Mean Squared Error)

Definition: RMSE is the square root of the average of the squared differences between the predicted and actual values.

Significance in Model Training:

• Balance between MAE and MSE: RMSE retains the sensitivity to outliers like MSE but brings the error metric back to the original scale of the data, making it more interpretable than MSE.
• Penalizes Large Errors: Similar to MSE, RMSE also penalizes larger errors more due to the squaring process, but because it takes the square root, it doesn’t exaggerate them as much as MSE does.
• Interpretable Units: Since RMSE is on the same scale as the original data, it’s easier to understand in the context of the problem. For instance, an RMSE of 5 means that on average, the model’s prediction errors are about 5 units away from the actual values.
• Optimization in Complex Models: RMSE is often used in models where the distribution of errors is important, such as in complex regression models or neural networks.

Visual Example to Show Significance in Model Training:

Let’s consider a graphical representation that shows how these metrics affect the model’s training process.

• MAE Focuses on Reducing Average Error: Imagine the model adjusting the regression line to minimize the average height of the gray dashed lines (errors) equally for all points.
• MSE Prioritizes Reducing Large Errors: The model might adjust the line more drastically to reduce the longer dashed lines (larger errors), even if it means increasing some smaller ones.
• RMSE Balances Both: The model will make adjustments that reduce large errors but will not overemphasize them to the extent of distorting the overall fit.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error

# Generate synthetic data with an outlier
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4   3 * X   np.random.randn(100, 1)
y[98] = 30  # Adding an outlier

# Train a simple linear regression model
model = LinearRegression()
model.fit(X, y)
y_pred = model.predict(X)

# Calculate MAE, MSE, and RMSE
mae = mean_absolute_error(y, y_pred)
mse = mean_squared_error(y, y_pred)
rmse = np.sqrt(mse)

# Plotting the regression line with errors
plt.figure(figsize=(12, 8))

# Scatter plot of actual data points
plt.scatter(X, y, color='blue', label='Actual Data')

# Regression line
plt.plot(X, y_pred, color='red', label='Regression Line')

# Highlighting errors (residuals)
for i in range(len(X)):
    plt.vlines(X[i], y[i], y_pred[i], color='gray', linestyle='dashed')

# Annotating one of the residual lines
plt.text(X[0]   0.1, (y[0]   y_pred[0]) / 2, 'Error (Residual)', color='gray')

# Adding annotations for MAE, MSE, RMSE
plt.text(0.5, 20, f'MAE: {mae:.2f}', fontsize=12, bbox=dict(facecolor='white', alpha=0.5))
plt.text(0.5, 18, f'MSE: {mse:.2f}', fontsize=12, bbox=dict(facecolor='white', alpha=0.5))
plt.text(0.5, 16, f'RMSE: {rmse:.2f}', fontsize=12, bbox=dict(facecolor='white', alpha=0.5))

# Titles and labels
plt.title('Linear Regression with MAE, MSE, and RMSE - Impact on Model Training')
plt.xlabel('X')
plt.ylabel('y')
plt.legend()
plt.show()

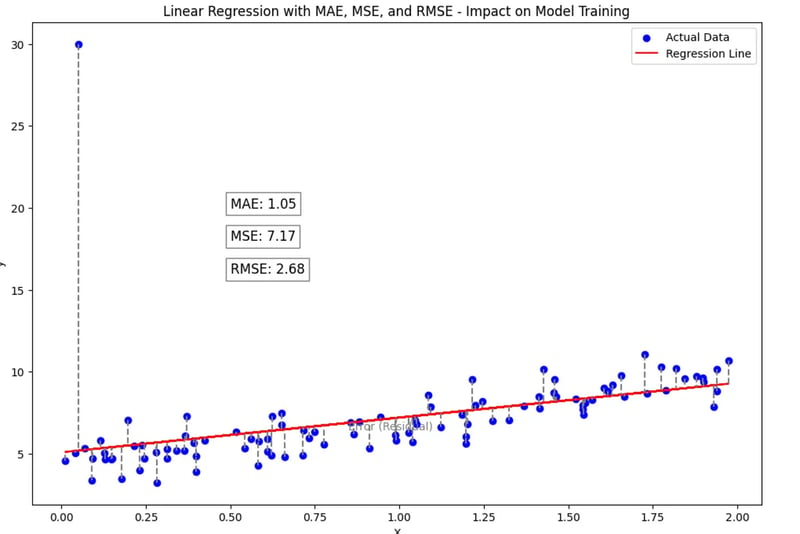
Explanation:

Outlier Impact: Notice how the model tries to adjust for the outlier in the upper region, which affects MSE and RMSE more significantly.

Model Training Implications:

• With MAE: The model may place less emphasis on the outlier, leading to a fit that is more balanced but less sensitive to extreme deviations.
• With MSE and RMSE: The model might adjust more aggressively to minimize the impact of the outlier, which can lead to a more distorted fit if outliers are rare.

Choosing the right approach for training a model depends on the specific problem you’re trying to solve, the nature of your data, and the goals of your model. Here’s a guide to help you decide which metric (MAE, MSE, RMSE) to focus on, along with considerations for training your model:

1. Nature of the Data

Presence of Outliers:

• MAE: If your data contains outliers, and you don’t want these outliers to disproportionately affect your model, MAE is a good choice. It treats all errors equally, so a few large errors won’t dominate the metric.
• MSE/RMSE: If outliers are expected and meaningful (e.g., extreme but valid cases), and you want your model to account for them strongly, MSE or RMSE might be more appropriate.

Homogeneous Data:

If your data is relatively homogeneous, without significant outliers, MSE or RMSE can help capture the overall performance, focusing more on the general fit of the model.

2. Goal of the Model

Interpretability:

• MAE: Offers easier interpretation since it’s in the same units as the target variable. If interpretability in the original units is essential, and you want to understand the average error in simple terms, MAE is preferable.
• RMSE: Also interpretable in the same units but with a focus on penalizing larger errors more.

Focus on Larger Errors:

• MSE/RMSE: If you care more about larger errors because they are particularly costly or risky in your application (e.g., predicting medical doses, financial forecasts), MSE or RMSE should be your focus. These metrics penalize larger errors more, which can guide the model to prioritize reducing significant deviations.
• MAE: If your application treats all errors equally and you don’t want the model to be overly concerned with large deviations, MAE is a better choice.

3. Model Type and Complexity

Simple Linear Models:

• MAE: Works well with simple linear models where the goal is to minimize the average deviation without worrying too much about outliers.
• MSE/RMSE: Can also be used, especially if the model is expected to account for all data points, including extreme cases.

Complex Models (e.g., Neural Networks, Ensemble Methods):

• MSE/RMSE: These are commonly used in more complex models because they provide a smoother gradient, which is essential for optimization techniques like gradient descent. The penalization of larger errors can also help in fine-tuning complex models.

4. Optimization and Convergence

Gradient Descent and Optimization:

• MSE/RMSE: Often preferred in optimization algorithms because they provide a smooth and continuous error surface, which is essential for methods like gradient descent to converge effectively.
• MAE: Can be less smooth, which might make optimization slightly more challenging, especially in large-scale models. However, modern optimization techniques can handle this in many cases.

5. Contextual Considerations

Application-Specific Requirements:

• MAE: Ideal for applications where you need to avoid the influence of outliers or when the cost of an error is linear, such as estimating delivery times or predicting scores.
• MSE/RMSE: Best for situations where large errors are particularly undesirable and where the application demands a higher penalty for these errors, such as in high-stakes financial predictions, safety-critical systems, or when optimizing models in competitive environments.

Conclusion: Which Approach to Take

• If Outliers are Not a Major Concern: Use MSE or RMSE. They help the model pay attention to larger errors, which can be crucial in many applications.
• If You Want a Balanced Approach: RMSE is often a good compromise, as it gives a measure in the same units as the target variable while still penalizing larger errors more than smaller ones.
• If You Need Robustness to Outliers: Use MAE. It ensures that outliers don’t disproportionately influence the model, making it suitable for situations where you want a more balanced model.
• For Interpretability in Original Units: MAE or RMSE are easier to interpret since they are in the same units as your target variable. This can be especially important in domains where you need to explain the results to non-technical stakeholders.

In practice, you might start with one metric based on these considerations and then experiment to see how your model performs with each. It’s also common to monitor multiple metrics during training to get a well-rounded view of your model’s performance.

Medium Article - Understanding MAE, MSE, and RMSE: Key Metrics in Machine Learning

@mondalsabbha