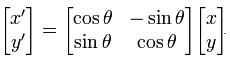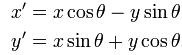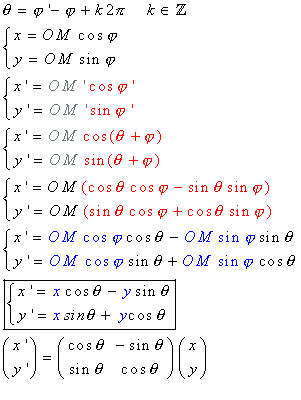TypeScript 中的函數式編程

Contents
- Introduction
- TypeScript Environment
- Representing Data Through Functions
- Sets
- Binary Operations
- Go Further
- Euclidean Plane
- Drawing a Disk
- Drawing Horizontal and Vertical Half-planes
- Functions
- Go Further
- Fractals
- Complex Numbers and Drawing
- Mandelbrot Fractal
- Go Further
You can find source code here: https://github.com/aelassas/functional-ts
Introduction
In TypeScript, functions are nothing but objects. Hence, functions can be constructed, passed as parameter, returned from functions or assigned into variables. Thus, TypeScript has first-class functions. More precisely, TypeScript supports the following:
- Higher-order functions arguments
- Higher-order functions results
- Nested functions
- Anonymous functions
- Closures
- Partial application (ECMAScript 5)
This article will not discuss the basics of functional programming, as you can find numerous resources on this topic on the Internet. Instead, it will talk about functional programming in TypeScript applied to algebra, numbers, the Euclidean plane, and fractals. The examples provided in this article will start from simple to more complex but always illustrated in a simple, straightforward and easy-to-understand manner.
TypeScript Environment
To run the source code, you'll need to install Node.js. Once Node.js is installed, download the source code archive, unzip it, go to the source code folder you unzipped on a terminal, set up TypeScript environment and install all necessary dependencies with the following command:
npm install
To run numbers' demo, run the following command:
npm run numbers
To run Euclidean plane's demo, run the following command:
npm run plane
To run fractals' demo, run the following command:
npm run fractals
Representing Data Through Functions
Let S be any set of elements a, b, c ... (for instance, the books on the table or the points of the Euclidean plane) and let S' be any subset of these elements (for instance, the green books on the table or the points in the circle of radius 1 centered at the origin of the Euclidean plane).
The Characteristic Function S'(x) of the set S' is a function which associates either true or false with each element x of S.
S'(x) = true if x is in S' S'(x) = false if x is not in S'
Let S be the set of books on the table and let S' be the set of green books on the table. Let a and b be two green books, and let c and d be two red books on the table. Then:
S'(a) = S'(b) = true S'(c) = S'(d) = false
Let S be the set of the points in the Euclidean plane and let S' be the set of the points in the circle of radius 1 centered at the origin of the Euclidean plane (0, 0) (unit circle). Let a and b be two points in the unit circle, and let c and d be two points in a circle of radius 2 centered at the origin of the Euclidean plane. Then:
S'(a) = S'(b) = true S'(c) = S'(d) = false
Thus, any set S' can always be represented by its Characteristic Function. A function that takes as argument an element and returns true if this element is in S', false otherwise. In other words, a set (abstract data type) can be represented through a function in TypeScript.
type Set= (x: T) => boolean
In the next sections, we will see how to represent some fundamental sets in the algebra of sets through TypeScript in a functional way, then we will define generic binary operations on sets. We will then apply these operations on numbers then on subsets of the Euclidean plane. Sets are abstract data structures, the subsets of numbers and the subsets of the Euclidean plane are the representation of abstract data-structures, and finally the binary operations are the generic logics that works on any representation of the abstract data structures.
Sets
This section introduces the representation of some fundamental sets in the algebra of sets through TypeScript.
Empty set

Let E be the empty set and Empty its Characteristic function. In algebra of sets, E is the unique set having no elements. Therefore, Empty can be defined as follows:
Empty(x) = false if x is in E Empty(x) = false if x is not in E
Thus, the representation of E in TypeScript can be defined as follows:
const empty = () => (e: T) => false
In algebra of sets, Empty is represented as follows:
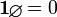
Thus, running the code below:
console.log('\nEmpty set:')
console.log('Is 7 in {}?', common.empty()(7))
gives the following results:

Set All

Let S be a set and S' be the subset of S that contains all the elements and All its Characteristic function. In algebra of sets, S' is the full set that contains all the elements. Therefore, All can be defined like this:
All(x) = true if x is in S
Thus, the representation of S' in TypeScript can be defined as follows:
const all = () => (e: T) => true
In algebra of sets, All is represented as follows:
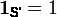
Thus, running the code below:
console.log('\nSet All:')
console.log('Is 7 in integers set?', common.all()(7))
gives the following results:

Singleton Set
Let E be the Singleton set and Singleton its Characteristic function. In algebra of sets, E also known as unit set, or 1-tuple is a set with exactly one element e. Therefore, Singleton can be defined as follows:
Singleton(x) = true if x is e Singleton(x) = false if x is not e
Thus, the representation of E in TypeScript can be defined as follows:
const singleton = (x: T) => (y: T) => x === y
Thus, running the code below:
console.log('\nSingleton set:')
console.log('Is 7 in the singleton set {0}?', common.singleton(0)(7))
console.log('Is 7 in the singleton set {7}?', common.singleton(7)(7)
gives the following results:

Other Sets
This section presents subsets of the integers set.
Even Numbers
Let E be the set of even numbers and Even its Characteristic function. In mathematics, an even number is a number which is a multiple of two. Therefore, Even can be defined as follows:
Even(x) = true if x is a multiple of 2 Even(x) = false if x is not a multiple of 2
Thus, the representation of E in TypeScript can be defined as follows:
const even = (x: number) => x % 2 === 0
Thus, running the code below:
console.log('\nEven numbers set:')
console.log('Is 99 in even numbers set?', numbers.even(99))
console.log('Is 998 in even numbers set?', numbers.even(998))
gives the following results:

Odd Numbers
Let E be the set of odd numbers and Odd its Characteristic function. In mathematics, an odd number is a number which is not a multiple of two. Therefore, Odd can be defined as follows:
Odd(x) = true if x is not a multiple of 2 Odd(x) = false if x is a multiple of 2
Thus, the representation of E in TypeScript can be defined as follows:
const odd = (x: number) => x % 2 === 1
Thus, running the code below:
console.log('\nOdd numbers set:')
console.log('Is 99 in odd numbers set?', numbers.odd(99))
console.log('Is 998 in odd numbers set?', numbers.odd(998))
gives the following results:

Multiples of 3
Let E be the set of multiples of 3 and MultipleOfThree its Characteristic function. In mathematics, a multiple of 3 is a number divisible by 3. Therefore, MultipleOfThree can be defined as follows:
MultipleOfThree(x) = true if x is divisible by 3 MultipleOfThree(x) = false if x is not divisible by 3
Thus, the representation of E in TypeScript can be defined as follows:
const multipleOfThree = (x: number) => x % 3 === 0
Thus, running the code below:
console.log('\nMultiples of 3 set:')
console.log('Is 99 in multiples of 3 set?', numbers.multipleOfThree(99))
console.log('Is 998 in multiples of 3 set?', numbers.multipleOfThree(998))
gives the following results:

Multiples of 5
Let E be the set of multiples of 5 and MultipleOfFive its Characteristic function. In mathematics, a multiple of 5 is a number divisible by 5. Therefore, MultipleOfFive can be defined as follows:
MultipleOfFive(x) = true if x is divisible by 5 MultipleOfFive(x) = false if x is not divisible by 5
Thus, the representation of E in TypeScript can be defined as follows:
const multipleOfFive = (x: number) => x % 5 === 0
Thus, running the code below:
console.log('\nMultiples of 5 set:')
console.log('Is 15 in multiples of 5 set?', numbers.multipleOfFive(15))
console.log('Is 998 in multiples of 5 set?', numbers.multipleOfFive(998))
gives the following results:

Prime Numbers
A long time ago, when I was playing with Project Euler problems, I had to resolve the following one:
By listing the first six prime numbers: 2, 3, 5, 7, 11, and 13, we can see that the 6th prime is 13. What is the 10 001st prime number?
To resolve this problem, I first had to write a fast algorithm that checks whether a given number is prime or not. Once the algorithm written, I wrote an iterative algorithm that iterates through primes until the 10 001st prime number was found.
Let E be the set of primes and Prime its Characteristic function. In mathematics, a prime is a natural number greater than 1 that has no positive divisors other than 1 and itself. Therefore, Prime can be defined as follows:
Prime(x) = true if x is prime Prime(x) = false if x is not prime
Thus, the representation of E in TypeScript can be defined as follows:
const prime = (x: number) => {
if (x
Thus, running the code below to resolve our problem:
console.log('\nPrimes set:')
console.log('Is 2 in primes set?', numbers.prime(2))
console.log('Is 4 in primes set?', numbers.prime(4))
console.log('The 10 001st prime number is', numbers.getPrime(10001))
where getPrime is defined below:
const getPrime = (p: number) => {
for (let i = 1, count = 0; ; i ) {
if (prime(i)) count
if (count === p) return i
}
}
gives the following results:

Binary Operations
This section presents several fundamental operations for constructing new sets from given sets and for manipulating sets. Below the Ven diagram in the algebra of sets.
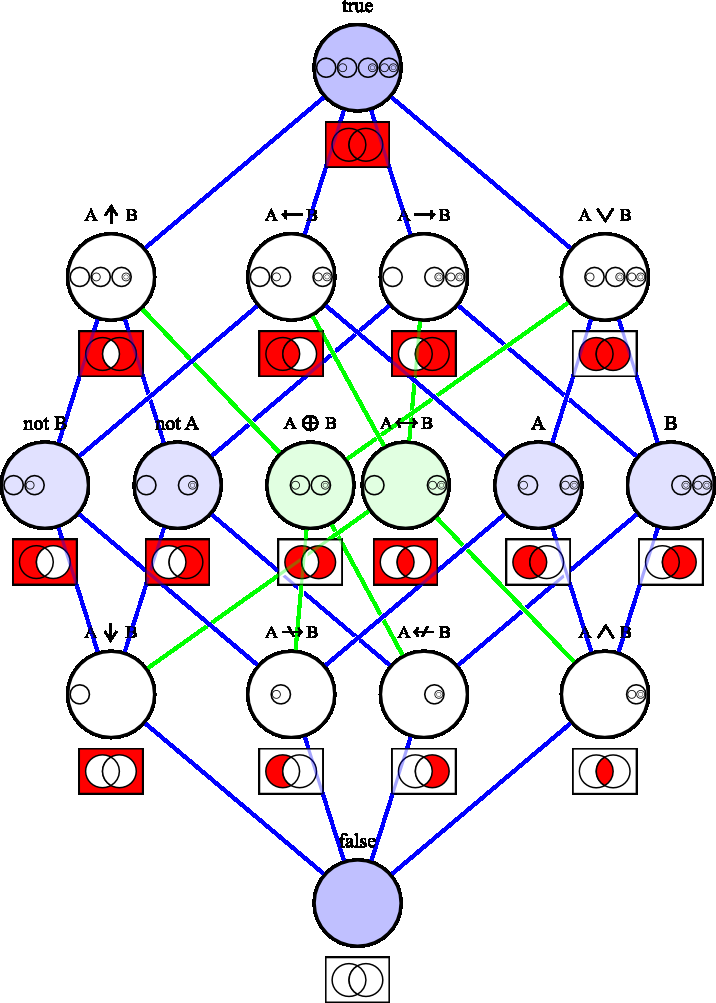
Union

Let E and F be two sets. The union of E and F, denoted by E U F is the set of all elements which are members of either E and F.
Let Union be the union operation. Thus, the Union operation can be implemented as follows in TypeScript:
const union = (e: Set, f: Set) => (x: T) => e(x) || f(x)
Running the code below:
console.log('\nUnion:')
console.log('Is 7 in the union of Even and Odd Integers Set?', core.union(numbers.even, numbers.odd)(7))
gives the following results:

Intersection
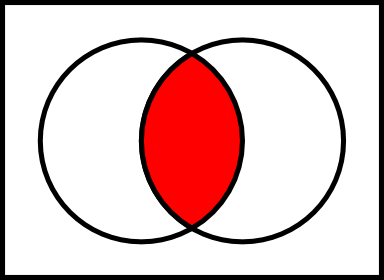
Let E and F be two sets. The intersection of E and F, denoted by E n F is the set of all elements which are members of both E and F.
Let Intersection be the intersection operation. Thus, the Intersection operation can be implemented as follows in TypeScript:
const intersection = (e: Set, f: Set) => (x: T) => e(x) && f(x)
Running the code below:
console.log('\nIntersection:')
const multiplesOfThreeAndFive = core.intersection(numbers.multipleOfThree, numbers.multipleOfFive)
console.log('Is 15 a multiple of 3 and 5?', multiplesOfThreeAndFive(15))
console.log('Is 10 a multiple of 3 and 5?', multiplesOfThreeAndFive(10))
gives the following results:

Cartesian Product
Let E and F be two sets. The cartesian product of E and F, denoted by E × F is the set of all ordered pairs (e, f) such that e is a member of E and f is a member of F.
Let CartesianProduct be the cartesian product operation. Thus, the CartesianProduct operation can be implemented as follows in TypeScript:
const cartesianProduct = (e: Set, f: Set) => (x: T1, y: T2) => e(x) && f(y)
Running the code below:
console.log('\nCartesian Product:')
const cp = core.cartesianProduct(numbers.multipleOfThree, numbers.multipleOfFive)
console.log('Is (9, 15) in MultipleOfThree x MultipleOfFive? ', cp(9, 15))
gives the following results:

Complements
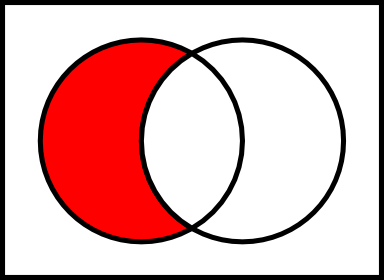
Let E and F be two sets. The relative complement of F in E, denoted by E \ F is the set of all elements which are members of E but not members of F.
Let Complement be the relative complement operation. Thus, the Complement operation can be implemented as follows in TypeScript:
const complement = (e: Set, f: Set) => (x: T) => e(x) && !f(x)
Running the code below:
console.log('\nComplement:')
const c = core.complement(numbers.multipleOfThree, numbers.multipleOfFive)
console.log('Is 15 in MultipleOfThree \\ MultipleOfFive set? ', c(15))
console.log('Is 9 in MultipleOfThree \\ MultipleOfFive set? ', c(9))
gives the following results:

Symmetric Difference
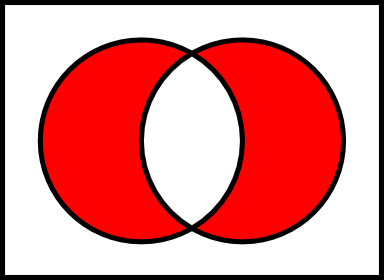
Let E and F be two sets. The symmetric difference of E and F, denoted by E Δ F is the set of all elements which are members of either E and F but not in the intersection of E and F.
Let SymmetricDifference be the symmetric difference operation. Thus, the SymmetricDifference operation can be implemented in two ways in TypeScript. A trivial way is to use the union and complement operations as follows:
const symmetricDifferenceWithoutXor = (e: Set, f: Set) =>
(x: T) => union(complement(e, f), complement(f, e))(x)
Another way is to use the XOR binary operation as follows:
const symmetricDifferenceWithXor = (e: Set, f: Set) => (x: T) => e(x) !== f(x)
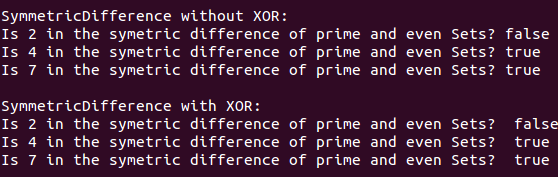
Running the code below:
console.log('\nSymmetricDifference without XOR:')
const sdWithoutXor = core.symmetricDifferenceWithoutXor(numbers.prime, numbers.even)
console.log('Is 2 in the symetric difference of prime and even Sets? ', sdWithoutXor(2))
console.log('Is 4 in the symetric difference of prime and even Sets? ', sdWithoutXor(4))
console.log('Is 7 in the symetric difference of prime and even Sets? ', sdWithoutXor(7))
console.log('\nSymmetricDifference with XOR:')
const sdWithXor = core.symmetricDifferenceWithXor(numbers.prime, numbers.even)
console.log('Is 2 in the symetric difference of prime and even Sets? ', sdWithXor(2))
console.log('Is 4 in the symetric difference of prime and even Sets? ', sdWithXor(4))
console.log('Is 7 in the symetric difference of prime and even Sets? ', sdWithXor(7))
gives the following results:
Other Operations
This section presents other useful binary operations on sets.
Contains
Let Contains be the operation that checks whether or not an element is in a set. This operation is a function that takes as parameter an element and returns true if the element is in the set, false otherwise.
Thus, this operation is defined as follows in TypeScript:
const contains = (e: Set, x: T) => e(x)
Therefore, running the code below:
console.log('\nContains:')
console.log('Is 7 in the singleton {0}? ', core.contains(common.singleton(0), 7))
console.log('Is 7 in the singleton {7}? ', core.contains(common.singleton(7), 7))
gives the following result:

Add
Let Add be the operation that adds an element to a set. This operation is a function that takes as parameter an element and adds it to the set.
Thus, this operation is defined as follows in TypeScript:
const add = (e: Set, y: T) => (x: T) => x === y || e(x)
Therefore, running the code below:
console.log('\nAdd:')
console.log('Is 7 in {0, 7}? ', core.add(common.singleton(0), 7)(7))
console.log('Is 0 in {1, 0}? ', core.add(common.singleton(1), 0)(0))
console.log('Is 7 in {19, 0}? ', core.add(common.singleton(19), 0)(7))
gives the following result:

Remove
Let Remove be the operation that removes an element from a set. This operations is a function that takes as parameter an element and removes it from the set.
Thus, this operation is defined as follows in TypeScript:
const remove = (e: Set, y: T) => (x: T) => x !== y && e(x)
Therefore, running the code below:
console.log('\nRemove:')
console.log('Is 7 in {}? ', core.remove(common.singleton(0), 0)(7))
console.log('Is 0 in {}? ', core.remove(common.singleton(7), 7)(0))
gives the following result:

For Those Who Want To Go Further
You can see how easy we can do some algebra of sets in TypeScript through Functional Programming. In the previous sections was shown the most fundamental definitions. But, If you want to go further, you can think about:
- Relations over sets
- Abstract algebra, such as monoids, groups, fields, rings, K-vectorial spaces and so on
- Inclusion-exclusion principle
- Russell's paradox
- Cantor's paradox
- Dual vector space
- Theorems and Corollaries
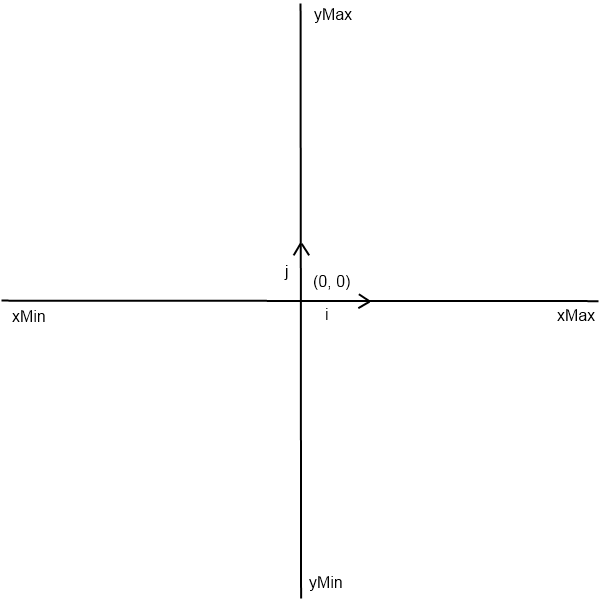
Euclidean Plane
In the previous section, the fundamental concepts on sets were implemented in TypeScript. In this section, we will practice the concepts implemented on the Euclidean plane.
Drawing a Disk
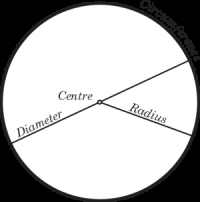
A disk is a subset of a plane bounded by a circle. There are two types of disks. Closed disks which are disks that contain the points of the circle that constitutes its boundary, and Open disks which are disks that do not contain the points of the circle that constitutes its boundary.
In this section, we will set up the Characterstic function of the Closed disk and draw it in a HTML5 page.
To set up the Characterstic function, we first need a function that calculates the Euclidean Distance between two points in the plane. This function is implemented as follows:
function distance(p1: Point, p2: Point) {
return Math.sqrt((p1.x - p2.x) ** 2 (p1.y - p2.y) ** 2)
}
where Point is defined below:
class Point {
x: number
y: number
constructor(x: number, y: number) {
this.x = x
this.y = y
}
}
This formula is based on Pythagoras' Theorem.
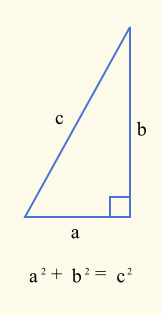
where c is the Euclidean distance, a² is (p1.X - p2.X)² and b² is (p1.Y - p2.Y)².
Let Disk be the Characteristic function of a closed disk. In algebra of sets, the definition of a closed disk in the reals set is as follows:

where a and b are the coordinates of the center and R the radius.
Thus, the implementation of Disk in TypeScript is as follows:
const disk = (center: Point, radius: number) => (p: Point) => distance(p, center)In order to view the set in a HTML5 page, I decided to implement a function draw that draws a set in the Euclidean plane. I chose HTML5 and thus used the canvas element for drawing.
Thus, I've built the Euclidean plane illustrated below through the method draw.
Below the implementation of the plane.
class Plane { width: number height: number constructor(width: number, height: number) { this.width = width this.height = height } draw(set: PlaneSet, canvasId: string) { const canvas = document.getElementById(canvasId) as HTMLCanvasElement if (!canvas) throw new Error(`Canvas with id ${canvasId} not found`) canvas.width = this.width canvas.height = this.height const context = canvas.getContext('2d') as CanvasRenderingContext2D const semiWidth = this.width / 2 const semiHeight = this.height / 2 const xMin = -semiWidth const xMax = semiWidth const yMin = -semiHeight const yMax = semiHeight for (let x = 0; xIn the draw function, a canvas having the same width and the same height as the Euclidean plane container is created. Then each point in pixels (x,y) of the canvas is replaced by a black point if it belongs to the set. xMin, xMax, yMin and yMax are the bounding values illustrated in the figure of the Euclidean plane above.
Running the code below:
euclideanPlane = new Plane(200, 200) euclideanPlane.draw(disk(new Point(0, 0), 50), 'disk')where disk is the id of the canvas:
gives the following result:
Drawing Horizontal and Vertical Half-planes
A horizontal or a vertical half-plane is either of the two subsets into which a plane divides the Euclidean space. A horizontal half-plane is either of the two subsets into which a plane divides the Euclidean space through a line perpendicular with the Y axis like in the figure above. A vertical half-plane is either of the two subsets into which a plane divides the Euclidean space through a line perpendicular with the X axis.
In this section, we will set up the Characteristic functions of the horizontal and vertical half-planes, draw them in a HTML5 page and see what we can do if we combine them with the disk subset.
Let HorizontalHalfPlane be the Characteristic function of a horizontal half-plane. The implementation of HorizontalHalfPlane in TypeScript is as follows:
const horizontalHalfPlane = (y: number, isLowerThan: boolean) => (p: Point) => (isLowerThan ? p.y = y)Thus, running the code below:
euclideanPlane.draw(horizontalHalfPlane(0, true),'hhp')where hhp is the id of the canvas:
gives the following result:
Let VerticalHalfPlane be the Characteristic function of a vertical half-plane. The implementation of VerticalHalfPlane in TypeScript is as follows:
const verticalHalfPlane = (x: number, isLowerThan: boolean) => (p: Point) => (isLowerThan ? p.x = x)Thus, running the code below:euclideanPlane.draw(verticalHalfPlane(0, false),'vhp')where vhd is the id of the canvas:
gives the following result:
In the first section of the article, we set up basic binary operations on sets. Thus, by combining the intersection of a disk and a half-plane for example, we can draw the half-disk subset.
Therefore, running the sample below:
euclideanPlane.draw(set.intersection(disk(new Point(0, 0), 50), verticalHalfPlane(0, false)), 'hd')where hd is the id of the canvas:
gives the following result:
Functions
This section presents functions on the sets in the Euclidean plane.
Translate
Let translatePoint be the function that translates a point in the plane. In Euclidean geometry, translatePoint is a function that moves a given point a constant distance in a specified direction. Thus the implementation in TypeScript is as follows:
const translatePoint = (deltax: number, deltay: number) => (p: Point) => new Point(p.x deltax, p.y deltay)where (deltax, deltay) is the constant vector of the translation.
Let translate be the function that translates a set in the plane. This function is simply implemented as follows in TypeScript:
const translate = (e: PlaneSet, deltax: number, deltay: number) => (p: Point) => e(translatePoint(-deltax, -deltay)(p))`translate` takes as parameters `deltax` which is the delta distance in the first Euclidean dimension and `deltay` which is the delta distance in the second Euclidean dimension. If a point _P (x, y)_ is translated in a set _S_, then its coordinates will change to _(x', y') = (x, delatx, y, deltay)_. Thus, the point _(x' - delatx, y' - deltay)_ will always belong to the set _S_. In set algebra, `translate` is called isomorph, in other words, the set of all translations forms the _translation group T_, which is isomorphic to the space itself. This explains the main logic of the function. Thus, running the code below in our HTML5 page:let translate_timer: ReturnType function translate_op() { let deltay = 0 clearTimeout(scale_timer) clearTimeout(rotate_timer) translate_timer = setInterval(() => { deltay = deltaywhere ep_op is the id of the canvas:
gives the following result:
Homothety
Let scalePoint be the function that sends any point M to another point N such that the segment SN is on the same line as SM, but scaled by a factor λ. In algebra of sets, Scale is formulated as follows:
Thus the implementation in TypeScript is as follows:
const scalePoint = (lambdax: number, lambday: number, deltax: number, deltay: number) => (p: Point) => new Point(lambdax * p.x deltax, lambday * p.y deltay)where (deltax, deltay) is the constant vector of the translation and (lambdax, lambday) is the lambda vector.
Let scale be the function that applies an homothety on a set in the plan. This function is simply implemented as follows in TypeScript:
const scale = (e: PlaneSet, lambdax: number, lambday: number, deltax: number, deltay: number) => (p: Point) => e(scalePoint(1 / lambdax, 1 / lambday, -deltax / lambdax, -deltay / lambday)(p))scale takes as parameters deltax which is the delta distance in the first Euclidean dimension, deltay which is the delta distance in the second Euclidean dimension and (lambdax, lambday) which is the constant factor vector λ. If a point P (x, y) is transformed through scale in a set S, then its coordinates will change to (x', y') = (lambdax * x, delatx, lambday * y, deltay). Thus, the point ((x'- delatx)/lambdax, (y' - deltay)/lambday) will always belong to the set S, If lambda is different from the vector 0, of course. In algebra of sets, scale is called isomorph, in other words, the set of all homotheties forms the Homothety group H, which is isomorphic to the space itself \ {0}. This explains the main logic of the function.
Thus, running the code below in our HTML5 page:
let scale_timer: ReturnType function scale_op() { let deltay = 0 let lambday = 0.05 clearTimeout(translate_timer) clearTimeout(rotate_timer) scale_timer = setInterval(() => { deltay = deltaygives the following result:
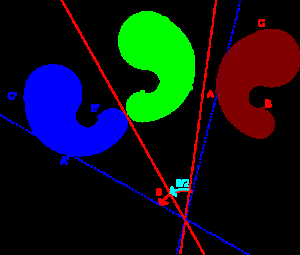
Rotate
Let rotatePoint be the function that rotates a point with an angle θ. In matrix algebra, rotatePoint is formulated as follows:
where (x', y') are the co-ordinates of the point after rotation, and the formula for x' and y' is as follows:
The demonstration of this formula is very simple. Have a look at this rotation.
Below the demonstration:
Thus the implementation in TypeScript is as follows:
const rotatePoint = (theta: number) => (p: Point) => new Point(p.x * Math.cos(theta) - p.y * Math.sin(theta), p.x * Math.sin(theta) p.y * Math.cos(theta))Let rotate be the function that applies a rotation on a set in the plane with the angle θ. This function is simply implemented as follows in TypeScript.
const rotate = (e: PlaneSet, theta: number) => (p: Point) => e(rotatePoint(-theta)(p))rotate is a function that takes as parameter theta which is the angle of the rotation. If a point P (x, y) is transformed through rotate in a set S, then its coordinates will change to (x', y') = (x * cos(theta) - y * sin(theta), x * sin(theta), y * cos(theta)). Thus, the point (x' * cos(theta), y' * sin(theta), y' * cos(theta) - x' * sin(theta)) will always belong to the set S. In algebra of sets, rotate is called isomorph, in other words, the set of all rotations forms the Rotation group R, which is isomorphic to the space itself. This explains the main logic of the function.
Thus, running the code below in our HTML5 page:
let rotate_timer: ReturnType function rotate_op() { let theta = 0 clearTimeout(translate_timer) clearTimeout(scale_timer) rotate_timer = setInterval(() => { euclideanPlane.draw(rotate(horizontalHalfPlane(-90, true), theta), 'ep_op') theta = (theta Math.PI / 2) % (2 * Math.PI) }, 1000) }gives the following result:
For Those Who Want to Go Further
Very simple, isn't it? For those who want to go further, you can explore these:
- Ellipse
- Three-dimensional Euclidean space
- Ellipsoide
- Paraboloid
- Hyperboloid
- Spherical harmonics
- Superellipsoid
- Haumea
- Homoeoid
- Focaloid
Fractals

Fractals are sets that have a fractal dimension that usually exceeds their topological dimension and may fall between the integers. For example, the Mandelbrot set is a fractal defined by a family of complex quadratic polynomials:
Pc(z) = z^2 c
where c is a complex. The Mandelbrot fractal is defined as the set of all points c such that the above sequence does not escape to infinity. In algebra of sets, this is formulated as follows:
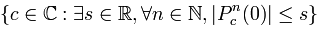
Fractals (abstract data type) can always be represented as follows in TypeScript:
type Fractal = (z: Complex, c: Complex) => Complex
Complex Numbers and Drawing
In order to be able to draw fractals, I needed to manipulate Complex numbers. Thus, I created the Complex class below:
class Complex {
x: number
y: number
static zero = new Complex(0, 0)
constructor(x: number, y: number) {
this.x = x
this.y = y
}
abs() {
return Math.sqrt(this.x * this.x this.y * this.y)
}
toString() {
return this.x ' i * ' this.y
}
}
function add(z1: Complex, z2: Complex) {
return new Complex(z1.x z2.x, z1.y z2.y)
}
function substract(z1: Complex, z2: Complex) {
return new Complex(z1.x - z2.x, z1.y - z2.y)
}
function multiply(z1: Complex, z2: Complex) {
return new Complex(z1.x * z2.x - z1.y * z2.y, z1.x * z2.y z1.y * z2.x)
}
Mandelbrot Fractal
I created a Mandelbrot Fractal (abstract data type representation) P(z) = z^2 c that is available below.
const mandelbrot = (z: Complex, c: Complex) => add(multiply(z, z), c)In order to be able to draw _Complex_ numbers, I created a `ComplexPlane` class. Below is the implementation in TypeScript.
class ComplexPlane {
width: number
height: number
real_min: number
real_max: number
imaginary_min: number
imaginary_max: number
boundary: number
fractalIterationsPerPixel: number
canvasId: string
constructor(
width: number,
height: number,
real_min: number,
real_max: number,
imaginary_min: number,
imaginary_max: number,
boundary: number,
fractalIterationsPerPixel: number,
canvasId: string,
) {
this.width = width
this.height = height
this.real_min = real_min
this.real_max = real_max
this.imaginary_min = imaginary_min
this.imaginary_max = imaginary_max
this.boundary = boundary
this.fractalIterationsPerPixel = fractalIterationsPerPixel
this.canvasId = canvasId
}
draw(fractal: Fractal) {
const canvas = document.getElementById(this.canvasId) as HTMLCanvasElement
canvas.width = this.width
canvas.height = this.height
const context = canvas.getContext('2d') as CanvasRenderingContext2D
context.fillStyle = 'white'
for (let x = 0; x
Thus, running the code below:
const complexPlane = new ComplexPlane(300, 300, -1.5, 1.5, -1.5, 1.5, 1.5, 20, 'fractal')
const mandelbrot = (z: Complex, c: Complex) => add(multiply(z, z), c)
complexPlane.pleaseWait()
setTimeout(() => complexPlane.draw(mandelbrot), 500)
where fractal is the id of the canvas:
gives the following result:

For Those Who Want to Go Further
For those who want to go further, you can explore these:
- Newton Fractals
- Julia Fractals
- Other Fractals
That's it! I hope you enjoyed reading.
-
 找到最大計數時,如何解決mySQL中的“組函數\”錯誤的“無效使用”?如何在mySQL中使用mySql 檢索最大計數,您可能會遇到一個問題,您可能會在嘗試使用以下命令:理解錯誤正確找到由名稱列分組的值的最大計數,請使用以下修改後的查詢: 計數(*)為c 來自EMP1 按名稱組 c desc訂購 限制1 查詢說明 select語句提取名稱列和每個名稱...程式設計 發佈於2025-07-13
找到最大計數時,如何解決mySQL中的“組函數\”錯誤的“無效使用”?如何在mySQL中使用mySql 檢索最大計數,您可能會遇到一個問題,您可能會在嘗試使用以下命令:理解錯誤正確找到由名稱列分組的值的最大計數,請使用以下修改後的查詢: 計數(*)為c 來自EMP1 按名稱組 c desc訂購 限制1 查詢說明 select語句提取名稱列和每個名稱...程式設計 發佈於2025-07-13 -
 CSS強類型語言解析您可以通过其强度或弱输入的方式对编程语言进行分类的方式之一。在这里,“键入”意味着是否在编译时已知变量。一个例子是一个场景,将整数(1)添加到包含整数(“ 1”)的字符串: result = 1 "1";包含整数的字符串可能是由带有许多运动部件的复杂逻辑套件无意间生成的。它也可以是故意从单个真理...程式設計 發佈於2025-07-13
CSS強類型語言解析您可以通过其强度或弱输入的方式对编程语言进行分类的方式之一。在这里,“键入”意味着是否在编译时已知变量。一个例子是一个场景,将整数(1)添加到包含整数(“ 1”)的字符串: result = 1 "1";包含整数的字符串可能是由带有许多运动部件的复杂逻辑套件无意间生成的。它也可以是故意从单个真理...程式設計 發佈於2025-07-13 -
 \“(1)vs.(;;):編譯器優化是否消除了性能差異?\”答案: 在大多數現代編譯器中,while(1)和(1)和(;;)之間沒有性能差異。編譯器: perl: 1 輸入 - > 2 2 NextState(Main 2 -E:1)V-> 3 9 Leaveloop VK/2-> A 3 toterloop(next-> 8 last-> 9 ...程式設計 發佈於2025-07-13
\“(1)vs.(;;):編譯器優化是否消除了性能差異?\”答案: 在大多數現代編譯器中,while(1)和(1)和(;;)之間沒有性能差異。編譯器: perl: 1 輸入 - > 2 2 NextState(Main 2 -E:1)V-> 3 9 Leaveloop VK/2-> A 3 toterloop(next-> 8 last-> 9 ...程式設計 發佈於2025-07-13 -
 PHP SimpleXML解析帶命名空間冒號的XML方法在php 很少,請使用該限制很大,很少有很高。例如:這種技術可確保可以通過遍歷XML樹和使用兒童()方法()方法的XML樹和切換名稱空間來訪問名稱空間內的元素。程式設計 發佈於2025-07-13
PHP SimpleXML解析帶命名空間冒號的XML方法在php 很少,請使用該限制很大,很少有很高。例如:這種技術可確保可以通過遍歷XML樹和使用兒童()方法()方法的XML樹和切換名稱空間來訪問名稱空間內的元素。程式設計 發佈於2025-07-13 -
 Java字符串非空且非null的有效檢查方法檢查字符串是否不是null而不是空的 if(str!= null && str.isementy())二手: if(str!= null && str.length()== 0) option 3:trim()。 isement(Isement() trim whitespace whites...程式設計 發佈於2025-07-13
Java字符串非空且非null的有效檢查方法檢查字符串是否不是null而不是空的 if(str!= null && str.isementy())二手: if(str!= null && str.length()== 0) option 3:trim()。 isement(Isement() trim whitespace whites...程式設計 發佈於2025-07-13 -
 解決Spring Security 4.1及以上版本CORS問題指南彈簧安全性cors filter:故障排除常見問題 在將Spring Security集成到現有項目中時,您可能會遇到與CORS相關的錯誤,如果像“訪問Control-allo-allow-Origin”之類的標頭,則無法設置在響應中。為了解決此問題,您可以實現自定義過濾器,例如代碼段中的MyFi...程式設計 發佈於2025-07-13
解決Spring Security 4.1及以上版本CORS問題指南彈簧安全性cors filter:故障排除常見問題 在將Spring Security集成到現有項目中時,您可能會遇到與CORS相關的錯誤,如果像“訪問Control-allo-allow-Origin”之類的標頭,則無法設置在響應中。為了解決此問題,您可以實現自定義過濾器,例如代碼段中的MyFi...程式設計 發佈於2025-07-13 -
 如何在無序集合中為元組實現通用哈希功能?在未訂購的集合中的元素要糾正此問題,一種方法是手動為特定元組類型定義哈希函數,例如: template template template 。 struct std :: hash { size_t operator()(std :: tuple const&tuple)const {...程式設計 發佈於2025-07-13
如何在無序集合中為元組實現通用哈希功能?在未訂購的集合中的元素要糾正此問題,一種方法是手動為特定元組類型定義哈希函數,例如: template template template 。 struct std :: hash { size_t operator()(std :: tuple const&tuple)const {...程式設計 發佈於2025-07-13 -
 Go語言如何動態發現導出包類型?與反射軟件包中的有限類型的發現能力相反,本文探索了替代方法,探索了在Runruntime。 go import( “ FMT” “去/進口商” ) func main(){ pkg,err:= incorter.default()。導入(“ time”) 如果er...程式設計 發佈於2025-07-13
Go語言如何動態發現導出包類型?與反射軟件包中的有限類型的發現能力相反,本文探索了替代方法,探索了在Runruntime。 go import( “ FMT” “去/進口商” ) func main(){ pkg,err:= incorter.default()。導入(“ time”) 如果er...程式設計 發佈於2025-07-13 -
 將圖片浮動到底部右側並環繞文字的技巧在Web設計中圍繞在Web設計中,有時可以將圖像浮動到頁面右下角,從而使文本圍繞它纏繞。這可以在有效地展示圖像的同時創建一個吸引人的視覺效果。 css位置在右下角,使用css float and clear properties: img { 浮點:對; ...程式設計 發佈於2025-07-13
將圖片浮動到底部右側並環繞文字的技巧在Web設計中圍繞在Web設計中,有時可以將圖像浮動到頁面右下角,從而使文本圍繞它纏繞。這可以在有效地展示圖像的同時創建一個吸引人的視覺效果。 css位置在右下角,使用css float and clear properties: img { 浮點:對; ...程式設計 發佈於2025-07-13 -
 如何高效地在一個事務中插入數據到多個MySQL表?mySQL插入到多個表中,該數據可能會產生意外的結果。雖然似乎有多個查詢可以解決問題,但將從用戶表的自動信息ID與配置文件表的手動用戶ID相關聯提出了挑戰。 使用Transactions和last_insert_id() 插入用戶(用戶名,密碼)值('test','tes...程式設計 發佈於2025-07-13
如何高效地在一個事務中插入數據到多個MySQL表?mySQL插入到多個表中,該數據可能會產生意外的結果。雖然似乎有多個查詢可以解決問題,但將從用戶表的自動信息ID與配置文件表的手動用戶ID相關聯提出了挑戰。 使用Transactions和last_insert_id() 插入用戶(用戶名,密碼)值('test','tes...程式設計 發佈於2025-07-13 -
 如何解決AppEngine中“無法猜測文件類型,使用application/octet-stream...”錯誤?appEngine靜態文件mime type override ,靜態文件處理程序有時可以覆蓋正確的mime類型,在錯誤消息中導致錯誤消息:“無法猜測mimeType for for file for file for [File]。 application/application/octet...程式設計 發佈於2025-07-13
如何解決AppEngine中“無法猜測文件類型,使用application/octet-stream...”錯誤?appEngine靜態文件mime type override ,靜態文件處理程序有時可以覆蓋正確的mime類型,在錯誤消息中導致錯誤消息:“無法猜測mimeType for for file for file for [File]。 application/application/octet...程式設計 發佈於2025-07-13 -
 如何正確使用與PDO參數的查詢一樣?在pdo 中使用類似QUERIES在PDO中的Queries時,您可能會遇到類似疑問中描述的問題:此查詢也可能不會返回結果,即使$ var1和$ var2包含有效的搜索詞。錯誤在於不正確包含%符號。 通過將變量包含在$ params數組中的%符號中,您確保將%字符正確替換到查詢中。沒有此修改,PD...程式設計 發佈於2025-07-13
如何正確使用與PDO參數的查詢一樣?在pdo 中使用類似QUERIES在PDO中的Queries時,您可能會遇到類似疑問中描述的問題:此查詢也可能不會返回結果,即使$ var1和$ var2包含有效的搜索詞。錯誤在於不正確包含%符號。 通過將變量包含在$ params數組中的%符號中,您確保將%字符正確替換到查詢中。沒有此修改,PD...程式設計 發佈於2025-07-13 -
 PHP未來:適應與創新PHP的未來將通過適應新技術趨勢和引入創新特性來實現:1)適應云計算、容器化和微服務架構,支持Docker和Kubernetes;2)引入JIT編譯器和枚舉類型,提升性能和數據處理效率;3)持續優化性能和推廣最佳實踐。 引言在編程世界中,PHP一直是網頁開發的中流砥柱。作為一個從1994年就開始發展...程式設計 發佈於2025-07-13
PHP未來:適應與創新PHP的未來將通過適應新技術趨勢和引入創新特性來實現:1)適應云計算、容器化和微服務架構,支持Docker和Kubernetes;2)引入JIT編譯器和枚舉類型,提升性能和數據處理效率;3)持續優化性能和推廣最佳實踐。 引言在編程世界中,PHP一直是網頁開發的中流砥柱。作為一個從1994年就開始發展...程式設計 發佈於2025-07-13 -
 在Ubuntu/linux上安裝mysql-python時,如何修復\“ mysql_config \”錯誤?mysql-python安裝錯誤:“ mysql_config找不到”“ 由於缺少MySQL開發庫而出現此錯誤。解決此問題,建議在Ubuntu上使用該分發的存儲庫。使用以下命令安裝Python-MysqldB: sudo apt-get安裝python-mysqldb sudo pip in...程式設計 發佈於2025-07-13
在Ubuntu/linux上安裝mysql-python時,如何修復\“ mysql_config \”錯誤?mysql-python安裝錯誤:“ mysql_config找不到”“ 由於缺少MySQL開發庫而出現此錯誤。解決此問題,建議在Ubuntu上使用該分發的存儲庫。使用以下命令安裝Python-MysqldB: sudo apt-get安裝python-mysqldb sudo pip in...程式設計 發佈於2025-07-13 -
 如何檢查對像是否具有Python中的特定屬性?方法來確定對象屬性存在尋求一種方法來驗證對像中特定屬性的存在。考慮以下示例,其中嘗試訪問不確定屬性會引起錯誤: >>> a = someClass() >>> A.property Trackback(最近的最新電話): 文件“ ”,第1行, AttributeError: SomeClass...程式設計 發佈於2025-07-13
如何檢查對像是否具有Python中的特定屬性?方法來確定對象屬性存在尋求一種方法來驗證對像中特定屬性的存在。考慮以下示例,其中嘗試訪問不確定屬性會引起錯誤: >>> a = someClass() >>> A.property Trackback(最近的最新電話): 文件“ ”,第1行, AttributeError: SomeClass...程式設計 發佈於2025-07-13
學習中文
- 1 走路用中文怎麼說? 走路中文發音,走路中文學習
- 2 坐飛機用中文怎麼說? 坐飞机中文發音,坐飞机中文學習
- 3 坐火車用中文怎麼說? 坐火车中文發音,坐火车中文學習
- 4 坐車用中文怎麼說? 坐车中文發音,坐车中文學習
- 5 開車用中文怎麼說? 开车中文發音,开车中文學習
- 6 游泳用中文怎麼說? 游泳中文發音,游泳中文學習
- 7 騎自行車用中文怎麼說? 骑自行车中文發音,骑自行车中文學習
- 8 你好用中文怎麼說? 你好中文發音,你好中文學習
- 9 謝謝用中文怎麼說? 谢谢中文發音,谢谢中文學習
- 10 How to say goodbye in Chinese? 再见Chinese pronunciation, 再见Chinese learning