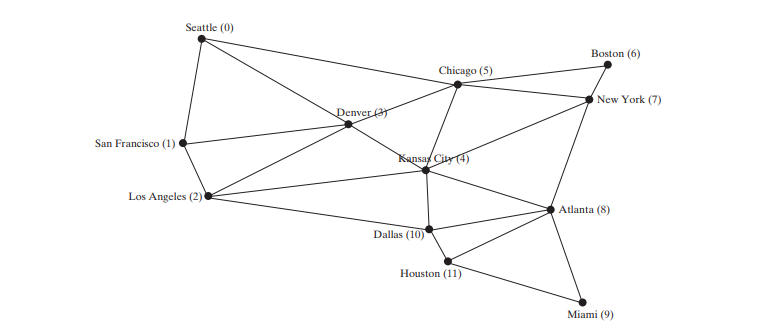
Многие реальные проблемы можно решить с помощью графовых алгоритмов. Графики полезны при моделировании и решении реальных проблем. Например, задачу поиска наименьшего количества рейсов между двумя городами можно смоделировать с помощью графа, вершины которого представляют города, а ребра — рейсы между двумя соседними городами, как показано на рисунке ниже. Задача поиска минимального количества стыковочных рейсов
между двумя городами сводится к поиску кратчайшего пути между двумя вершинами графа.

Изучение задач на графах известно как теория графов. Теория графов была основана Леонардом Эйлером в 1736 году, когда он ввел терминологию графов для решения знаменитой задачи Семи мостов Кенигсберга. Город Кенигсберг в Пруссии (ныне Калининград, Россия) был разделен рекой Прегель. На реке было два острова. Город и острова были соединены семью мостами, как показано на рисунке ниже (а). Вопрос в том, можно ли прогуляться, пересечь каждый мост ровно один раз и вернуться в исходную точку? Эйлер доказал, что это невозможно.

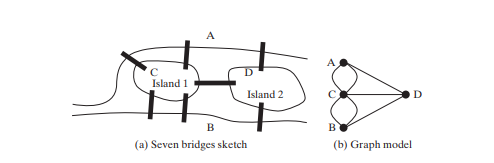
Чтобы доказать это, Эйлер сначала абстрагировал карту города Кенигсберга, удалив все улицы, и получил эскиз, показанный на рисунке выше (a). Затем он заменил каждый участок суши точкой, называемой вершиной или узлом, а каждый мост линией, называемой краем, как показано на рис. Рисунок выше (б). Эта структура с вершинами и ребрами называется графом.

Глядя на граф, мы спрашиваем, существует ли путь, начинающийся из любой вершины, проходящий все ребра ровно один раз и возвращающийся в начальную вершину. Эйлер доказал, что для существования такого пути каждая вершина должна иметь четное число ребер. Следовательно, задача о семи мостах Кенигсберга не имеет решения.

Задачи с графами часто решаются с помощью алгоритмов. Графовые алгоритмы имеют множество применений в различных областях, например, в информатике, математике, биологии, инженерии, экономике, генетике и социальных науках.

Базовая терминология графов

Граф состоит из вершин и ребер, соединяющих вершины. В этой главе не предполагается, что у вас есть какие-либо предварительные знания в области теории графов или дискретной математики. Для определения графиков мы используем простые и понятные термины.

Что такое график? Граф — это математическая структура, которая представляет отношения между объектами реального мира. Например, график на рисунке выше представляет полеты между городами, а график на рисунке ниже (b) представляет мосты между сухопутными массивами.

Граф состоит из непустого набора вершин (также известного как узлы или точки) и набора ребер, соединяющих вершины. Для удобства мы определяем граф как G = (V, E), где V представляет собой набор вершин, а E представляет собой набор ребер. Например, V и E для графика на рисунке ниже выглядят следующим образом:

V = {"Сиэтл", "Сан-Франциско", "Лос-Анджелес",
«Денвер», «Канзас-Сити», «Чикаго», «Бостон», «Нью-Йорк»,
«Атланта», «Майами», «Даллас», «Хьюстон»};

E = {{"Сиэтл", "Сан-Франциско"},{"Сиэтл", "Чикаго"},
{"Сиэтл", "Денвер"}, {"Сан-Франциско", "Денвер"},
...
};

График может быть ориентированным и неориентированным. В ориентированном графе каждое ребро имеет направление, которое указывает, что через ребро можно перемещаться от одной вершины к другой. Вы можете моделировать отношения родитель/потомок с помощью ориентированного графа, где ребро от вершины A до B указывает, что A является родительским элементом B. На рисунке ниже (a) показан ориентированный граф.

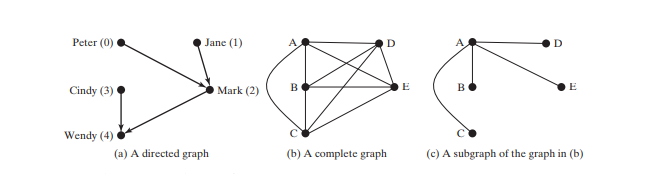
В неориентированном графе вы можете перемещаться между вершинами в обоих направлениях. Граф на рисунке ниже неориентированный.

Ребра могут быть взвешенными или невзвешенными. Например, вы можете присвоить вес каждому ребру на графике на рисунке выше, чтобы указать время полета между двумя городами.

Две вершины графа называются смежными, если они соединены одним и тем же ребром. Аналогично, два ребра называются смежными, если они соединены с одной и той же вершиной. Ребро в графе, соединяющее две вершины, называется инцидентным с обеими вершинами. Степень вершины — это количество инцидентных ей ребер.

Две вершины называются соседями, если они смежны. Аналогично, два ребра называются соседями, если они смежны.

Петля — это ребро, связывающее вершину с самой собой. Если две вершины соединены двумя или более ребрами, эти ребра называются параллельными ребрами. простой граф — это граф, в котором нет петель и параллельных ребер. В полном графе каждые две пары вершин соединены, как показано на рисунке ниже (b).

Граф является связным, если между любыми двумя вершинами графа существует путь. подграф графа G — это граф, множество вершин которого является подмножеством множества вершин графа G, а множество ребер является подмножеством графа G. Например, граф на рисунке выше (c) представляет собой подграф графика на рисунке выше (b).

Предположим, что граф связный и неориентированный. цикл — это замкнутый путь, который начинается из вершины и заканчивается в той же вершине. Связный граф является деревом, если в нем нет циклов. остовное дерево графа G — это связный подграф графа G, а этот подграф — это дерево, содержащее все вершины из G.