No mundo acelerado das finanças, a precisão é tudo. É sempre melhor evitar uma perda de um milhão de dólares devido a um erro de arredondamento/precisão.

Quando se trata de dinheiro, pense no tipo de dados

O ponto de partida deste artigo é a compreensão de que dinheiro não é o número básico médio que você pode usar para contar as maçãs em sua cesta. O que você ganha quando tenta multiplicar 10€ por 10$? Difícil né… Você já encontrou milagrosos US$ 1.546 no bolso de uma jaqueta velha? Sim, eu sei, isso também não é possível. Esses exemplos bobos estão aqui para ilustrar o fato de que o dinheiro tem suas próprias regras particulares e não pode ser modelado apenas por um simples número. Garanto-lhe que não fui o primeiro a perceber isso (e talvez você tenha percebido muito antes de mim). Em 2002, o programador Martin Fowler propôs no Patterns of Enterprise Application Architecture uma forma de representar dinheiro, com atributos e regras de operandos específicos. Para ele, os dois atributos mínimos viáveis ​​necessários para um tipo de dados monetário eram:

amount
currency

Esta representação realmente básica será nosso ponto de partida para construir um modelo monetário simples, mas robusto.

Valores em dinheiro, como representá-los

Uma quantia em dinheiro é definitivamente um número específico: tem uma precisão fixa (novamente, você não pode ter 4.376$ no bolso). Você precisa escolher uma forma de representá-lo que o ajude a respeitar essa restrição.

Uma abordagem ingênua, o tipo de dados JavaScript de número nativo

Alerta de spoiler, definitivamente não é uma boa ideia se você não quiser ver alguns centavos (se não forem dólares) desaparecerem no mundo sombrio da representação de números de pontos flutuantes.

O caro erro de precisão

Se você tem alguma experiência com codificação em JavaScript, sabe que mesmo o cálculo mais simples pode resultar em um erro de precisão que você não esperaria a princípio. O exemplo mais óbvio e conhecido para destacar esse fenômeno é:

0.1   0.2 !== 0.3 // true
0.1   0.2 // 0.30000000000000004

Se este exemplo não o convencer totalmente, aconselho você a dar uma olhada neste artigo, que se aprofunda um pouco mais em todos os resultados de cálculo problemáticos que você pode encontrar ao trabalhar com o tipo de número nativo JavaScript…

Este ligeiro delta nos resultados pode parecer inofensivo para você (com uma magnitude de cerca de ~ 10^-16), no entanto, em uma aplicação financeira crítica, tal erro pode se espalhar rapidamente. Considere transferir fundos entre milhares de contas, onde cada transação envolve cálculos semelhantes. As pequenas imprecisões se somam e, antes que você perceba, suas demonstrações financeiras estão erradas em milhares de dólares. E honestamente, todos podemos concordar que quando se trata de dinheiro, o erro não é permitido: tanto legalmente como para construir uma relação de confiança com os seus clientes.

Por que tal erro?

A primeira pergunta que me fiz ao encontrar o problema em um dos meus projetos é por que ? Descobri que a origem do problema não é JavaScript e essas imprecisões também afetam outras linguagens de programação modernas (Java, C, Python, …).

// In C
#include 

int main() {
    double a = 0.1;
    double b = 0.2;
    double sum = a   b;
    if (sum == 0.3) {
        printf("Equal\n");
    } else {
        printf("Not Equal\n"); // This block is executed
    }
    return 0;
}

// > Not equal

// In Java
public class doublePrecision {
    public static void main(String[] args) {

        double total = 0;
        total  = 5.6;
        total  = 5.8;
        System.out.println(total);
    }
}

// > 11.399999999999

Na verdade, a causa raiz está no padrão usado por essas linguagens para representar números de ponto flutuante: o formato de ponto flutuante de precisão dupla (ou simples), especificado pelo padrão IEEE 754.

Padrão IEEE 754: uma história de representação de bits

Em Javascript, o tipo nativo number corresponde a números de ponto flutuante de precisão dupla, o que significa que um número é codificado com 64 bits e dividido em três partes:

• 1 bit para o sinal
• 11 bits para o expoente
• 52 bits para a mantissa (ou fração) que varia de 0 a 1

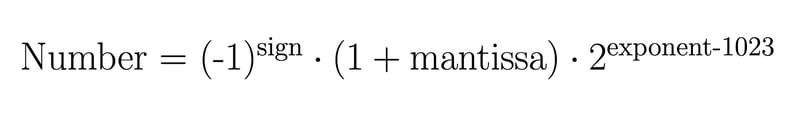
Então, você precisa usar a seguinte fórmula para converter sua representação de bits em um valor decimal:

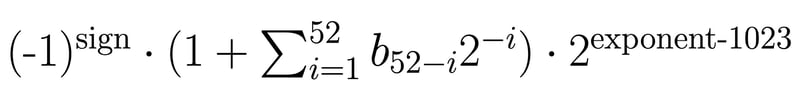
Um exemplo de representação de número de ponto flutuante de precisão dupla, uma aproximação de 1/3 :

0 01111111101 0101010101010101010101010101010101010101010101010101

= (-1)^0 x (1   2^-2   2^-4   2^-6   ...   2^-50   2^-52) x 2^(1021-1023)
= 0.333333333333333314829616256247390992939472198486328125
~ 1/3

Este formato nos permite representar uma vasta gama de valores, mas não pode representar todos os números possíveis com precisão absoluta (apenas entre 0 e 1 você pode encontrar uma infinidade de números…). Muitos números não podem ser representados exatamente na forma binária. Para repetir o primeiro exemplo, esse é o problema com 0,1 e 0,2. A representação flutuante de ponto duplo nos dá uma aproximação desses valores, portanto, quando você adiciona essas duas representações imprecisas, o resultado também não é exato.

Uma possível solução: Aritmética Decimal Arbitrária

Agora que você está totalmente convencido de que lidar com quantias de dinheiro com tipo de número JavaScript nativo é uma má ideia (pelo menos espero que você comece a ter dúvidas sobre isso), a pergunta de 1 bilhão de dólares é como você deve proceder ? Uma solução poderia ser usar alguns dos poderosos pacotes aritméticos de precisão fixa disponíveis em JavaScript. Por exemplo Decimal.js (que é usado pelo popular ORM Prisma para representar seu tipo de dados Decimal) ou Big.js.

Esses pacotes fornecem tipos de dados especiais que permitem realizar cálculos eliminando os erros de precisão que explicamos acima.

// Example using Decimal.js
const Decimal = require('decimal.js');
const a = new Decimal('0.1');
const b = new Decimal('0.2');
const result = a.plus(b);

console.log(result.toString()); // Output: '0.3'

Essa abordagem oferece outra vantagem: estende drasticamente o valor máximo que pode ser representado, o que pode se tornar muito útil quando você está lidando com criptomoedas, por exemplo.
Mesmo que seja realmente robusto, não é o que prefiro escolher para implementar nas minhas aplicações web. Acho mais fácil e claro aplicar a estratégia Stripe para lidar apenas com valores inteiros.

Aprenda com os mestres: Stripe, uma estratégia sem pontos flutuantes

Nós, da Theodo Fintech, valorizamos o pragmatismo! Adoramos nos inspirar nas empresas de maior sucesso do setor. Stripe, a conhecida empresa de bilhões de dólares especializada em serviços de pagamento, optou por lidar com quantias de dinheiro sem números flutuantes, mas com números inteiros. Para fazer isso, eles usam a menor unidade da moeda para representar um valor monetário.

// 10 USD are represented by
{
 "amount": 1000,
 "currency": "USD"
}

As unidades mínimas da moeda… não são consistentes!

Acho que muitos de vocês já sabem disso: nem todas as moedas têm a menor unidade da mesma magnitude. A maioria delas são moedas com “duas casas decimais” (EUR, USD, GBP), o que significa que a sua menor unidade é 1/100 da moeda. No entanto, algumas são moedas de “três decimais” (KWD) ou mesmo moedas de “zero decimal” (JPY). (Você pode encontrar mais informações sobre isso seguindo o padrão ISO4217). Para lidar com essas disparidades, você deve integrar à sua representação de dados monetários o fator multiplicativo para converter um valor representado na menor unidade na moeda correspondente.

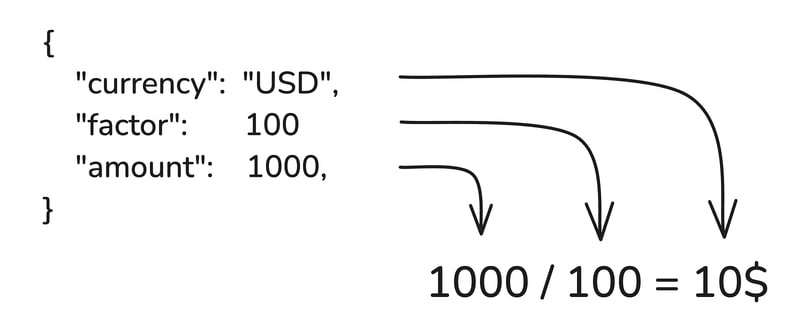
Escolhi uma maneira de representar o valor em dinheiro... OK, mas agora, como faço para arredondá-lo?

Acho que você já descobriu: você pode trabalhar com números nativos, pacotes de precisão arbitrária de terceiros ou números inteiros. Os cálculos podem (e irão) levar você a resultados de ponto flutuante que você precisará arredondar para seu valor monetário precisão finita. Como um exemplo rápido nunca é demais, digamos que você lida com valores inteiros e contratou um empréstimo de 16k$ com uma taxa de juros bem precisa de 8,5413% (ai…). Você então precisará reembolsar 16k$ mais uma quantia adicional de

1600000 * 0.085413 // amount in cents
//Output in cents: 136660.8

O ponto crucial é lidar adequadamente com o processo de arredondamento de valores monetários após os cálculos. Na maioria das vezes, você acaba tendo que escolher entre três tipos diferentes de arredondamento:

• Arredondamento clássico: Arredonde para o valor mais próximo e se estiver no meio do caminho entre dois valores, arredonde para cima
• Arredondamento do banqueiro: Arredonde para o valor mais próximo e se estiver no meio do caminho entre dois valores, arredonde para baixo se o número for par e arredonde para cima se o número for ímpar (isso lhe dá estabilidade numérica quando você tem que realizar muitos arredondamento)
• Arredondamento personalizado: com base na legislação específica da moeda que você usa e do caso de uso que você está tratando

Quando se trata de arredondamentos, não existe realmente nenhum "molho mágico": você precisa arbitrar dependendo da sua situação. Recomendo que você sempre verifique a legislação ao lidar com uma nova moeda e um novo caso de uso de arredondamento (conversão, divisão de dinheiro, taxas de juros para créditos, …). É melhor você seguir os regulamentos imediatamente para evitar mais problemas. Por exemplo, quando se trata de taxas de conversão, a maioria das moedas tem regras determinadas sobre a precisão necessária e regras de arredondamento (você pode dar uma olhada nas regras de taxa de conversão do EUR aqui).

Conclusão

Este artigo não é exaustivo sobre todas as possibilidades existentes para lidar com quantias de dinheiro em JavaScript e também não tem como objetivo fornecer um modelo de dados de dinheiro completo/perfeito. Tentei dar-lhe dicas e orientações suficientes para implementar uma representação que se revelou consistente, resiliente e que foi escolhida por grandes atores da indústria fintech. Espero que você consiga realizar cálculos de quantias em dinheiro em seus projetos futuros sem esquecer nenhum centavo no bolso (caso contrário, não se esqueça de dar uma olhada em sua jaqueta velha)!