분할 정복을 사용하여 가장 가까운 점 쌍 찾기
이 섹션에서는 분할 정복을 사용하여 가장 가까운 점 쌍을 찾는 효율적인 알고리즘을 제시합니다. 일련의 점들이 주어졌을 때 가장 가까운 쌍 문제는 서로 가장 가까운 두 점을 찾는 것입니다. 아래 그림과 같이 가장 가까운 쌍 애니메이션에서는 가장 가까운 두 지점을 연결하는 선이 그려집니다.
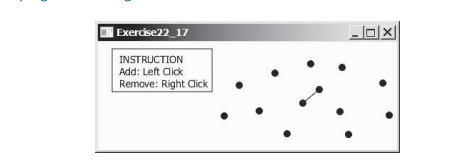
사례 연구: 가장 가까운 쌍 찾기에서는 가장 가까운 점 쌍을 찾기 위한 무차별 대입 알고리즘을 제시했습니다. 알고리즘은 모든 점 쌍 사이의 거리를 계산하고 거리가 최소인 점을 찾습니다. 분명히 알고리즘은 O(n^2) 시간이 걸립니다. 보다 효율적인 알고리즘을 설계할 수 있나요?
우리는 이 문제를 해결하기 위해 분할 정복이라는 접근 방식을 사용할 것입니다. 이 접근 방식은 문제를 하위 문제로 나누고 하위 문제를 해결한 다음 하위 문제의 솔루션을 결합하여 전체 문제에 대한 솔루션을 얻습니다. 동적 프로그래밍 접근 방식과 달리 분할 정복 접근 방식의 하위 문제는 겹치지 않습니다. 하위 문제는 크기가 더 작은 원래 문제와 같으므로 재귀를 적용하여 문제를 해결할 수 있습니다. 실제로 재귀 문제에 대한 모든 솔루션은 분할 정복 접근 방식을 따릅니다.
아래 단계에서는 분할 정복 접근법을 사용하여 가장 가까운 쌍 문제를 해결하는 방법을 설명합니다.
- 1단계: x 좌표의 오름차순으로 점을 정렬합니다. 동일한 x 좌표를 가진 점의 경우 y 좌표를 기준으로 정렬합니다. 결과적으로 정렬된 S개의 포인트 목록이 생성됩니다.
- 2단계: 정렬된 목록의 중간점을 사용하여 S를 동일한 크기의 두 하위 집합 S1과 S2로 나눕니다. 중간점을 S1에 두십시오. S1과 S2에서 가장 가까운 쌍을 재귀적으로 찾습니다. d1과 d2는 각각 두 하위 집합에서 가장 가까운 쌍의 거리를 나타냅니다.
- 3단계: S1의 한 점과 S2의 한 점 사이에서 가장 가까운 쌍을 찾고 그 거리를 d3으로 표시합니다. 가장 가까운 쌍은 거리가 min(d1, d2, d3)인 쌍입니다.
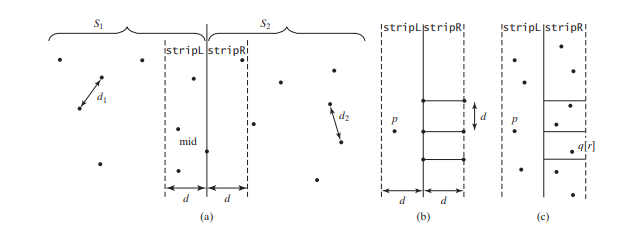
선택 정렬에는 O(n^2) 시간이 걸립니다. 1단계는 O(n log n) 시간 안에 완료될 수 있습니다. 3단계는 O(n) 시간 안에 완료할 수 있습니다. d = 최소(d1, d2)라고 가정합니다. 우리는 가장 가까운 쌍 거리가 d보다 클 수 없다는 것을 이미 알고 있습니다. S1의 포인트와 S2의 포인트가 S에서 가장 가까운 쌍을 형성하려면 아래 그림과 같이 왼쪽 포인트는 stripL에 있고 오른쪽 포인트는 stripR에 있어야 합니다( ㅏ).
stripL의 점 p에 대해 아래 (b)와 같이 d X 2d 직사각형 내의 오른쪽 점만 고려하면 됩니다. 직사각형 외부의 오른쪽 점은 p와 가장 가까운 쌍을 형성할 수 없습니다. S2의 가장 가까운 쌍 거리는 d보다 크거나 같으므로 최대 6개의
가 있을 수 있습니다.
직사각형의 점. 따라서 stripL의 각 지점에 대해 stripR의 최대 6개 지점을 고려해야 합니다.
stripL의 각 점 p에 대해 stripR의 해당 d X 2d 직사각형 영역에서 점을 어떻게 찾습니까? stripL 및 stripR의 포인트가 y 좌표의 오름차순으로 정렬되면 이 작업을 효율적으로 수행할 수 있습니다. pointsOrderedOnY를 y 좌표의 오름차순으로 정렬된 포인트 목록으로 둡니다. pointsOrderedOnY는 알고리즘에서 미리 얻을 수 있습니다. stripL 및 stripR는 아래 코드와 같이 3단계의 pointsOrderedOnY에서 얻을 수 있습니다.
pointOrderedOnY의 각 포인트 p에 대해
if (p는 S1에 있고 mid.x – p.x
p를 StripL에 추가;
else if (p는 S2에 있고 p.x - mid.x
p를 p를 추가하여 StripR;
다음과 같이 stripL 및 stripR의 점을 {p0, p1, ... , pk} 및 {q0, q1, ... , qt}로 둡니다. 위의 그림 (c). stripL의 점과 stripR의 점 사이의 가장 가까운 쌍은 아래 코드에 설명된 알고리즘을 사용하여 찾을 수 있습니다.
d = min(d1, d2);
r = 0; // r is the index of a point in stripR
for (each point p in stripL) {
// Skip the points in stripR below p.y - d
while (r
stripL의 포인트는 p0, p1, ... , pk 순으로 고려됩니다. stripL의 점 p에 대해 p.y – d 아래에 있는 stripR의 점을 건너뜁니다(5-6행). 한 지점을 건너뛰면 더 이상 고려되지 않습니다. while 루프(9~17행)는 (p, q[r1])가 가능한 가장 가까운 쌍인지 확인합니다. 이러한 q[r1] 쌍은 최대 6개입니다. stripR의 두 점 사이의 거리는 d보다 작을 수 없기 때문입니다. 따라서 3단계에서 가장 가까운 쌍을 찾는 복잡성은 O(n)입니다.
위 단계의 1단계는 포인트를 사전 정렬하기 위해 한 번만 수행됩니다. 모든 점이 미리 정렬되어 있다고 가정합니다. T(n)은 이 알고리즘의 시간 복잡도를 나타냅니다. 따라서,
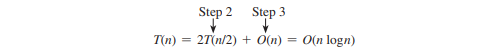
따라서 가장 가까운 점 쌍은 O(n log n) 시간에 찾을 수 있습니다.
-
 JavaScript 객체에서 키를 동적으로 설정하는 방법은 무엇입니까?jsobj = 'example'1; jsObj['key' i] = 'example' 1; 배열은 특수한 유형의 객체입니다. 그것들은 숫자 특성 (인치) + 1의 수를 반영하는 길이 속성을 유지합니다. 이 특별한 동작은 표준 객체에...프로그램 작성 2025-05-05에 게시되었습니다
JavaScript 객체에서 키를 동적으로 설정하는 방법은 무엇입니까?jsobj = 'example'1; jsObj['key' i] = 'example' 1; 배열은 특수한 유형의 객체입니다. 그것들은 숫자 특성 (인치) + 1의 수를 반영하는 길이 속성을 유지합니다. 이 특별한 동작은 표준 객체에...프로그램 작성 2025-05-05에 게시되었습니다 -
 Point-In-Polygon 감지에 더 효율적인 방법 : Ray Tracing 또는 Matplotlib \ 's Path.contains_points?Ray Tracing MethodThe ray tracing method intersects a horizontal ray from the point under examination with the polygon's sides. 교차로의 수를 계산하고 지점이 패...프로그램 작성 2025-05-05에 게시되었습니다
Point-In-Polygon 감지에 더 효율적인 방법 : Ray Tracing 또는 Matplotlib \ 's Path.contains_points?Ray Tracing MethodThe ray tracing method intersects a horizontal ray from the point under examination with the polygon's sides. 교차로의 수를 계산하고 지점이 패...프로그램 작성 2025-05-05에 게시되었습니다 -
 Fastapi Custom 404 페이지 제작 가이드custom 404 fastapi 가없는 페이지를 찾을 수 없습니다. 적절한 방법은 특정 요구 사항에 따라 다릅니다. 404 상태 코드에서 리디렉션 response = await call_next(request) if response.sta...프로그램 작성 2025-05-05에 게시되었습니다
Fastapi Custom 404 페이지 제작 가이드custom 404 fastapi 가없는 페이지를 찾을 수 없습니다. 적절한 방법은 특정 요구 사항에 따라 다릅니다. 404 상태 코드에서 리디렉션 response = await call_next(request) if response.sta...프로그램 작성 2025-05-05에 게시되었습니다 -
 Visual Studio 2012의 DataSource 대화 상자에 MySQL 데이터베이스를 추가하는 방법은 무엇입니까?MySQL 커넥터 v.6.5.4가 설치되어 있지만 Entity 프레임 워크의 DataSource 대화 상자에 MySQL 데이터베이스를 추가 할 수 없습니다. 이를 해결하기 위해 MySQL 용 공식 Visual Studio 2012 통합은 MySQL 커넥터 v.6....프로그램 작성 2025-05-05에 게시되었습니다
Visual Studio 2012의 DataSource 대화 상자에 MySQL 데이터베이스를 추가하는 방법은 무엇입니까?MySQL 커넥터 v.6.5.4가 설치되어 있지만 Entity 프레임 워크의 DataSource 대화 상자에 MySQL 데이터베이스를 추가 할 수 없습니다. 이를 해결하기 위해 MySQL 용 공식 Visual Studio 2012 통합은 MySQL 커넥터 v.6....프로그램 작성 2025-05-05에 게시되었습니다 -
 Homebrew에서 GO를 설정하면 명령 줄 실행 문제가 발생하는 이유는 무엇입니까?발생하는 문제를 해결하려면 다음을 수행하십시오. 1. 필요한 디렉토리 만들기 mkdir $ home/go mkdir -p $ home/go/src/github.com/user 2. 환경 변수 구성프로그램 작성 2025-05-05에 게시되었습니다
Homebrew에서 GO를 설정하면 명령 줄 실행 문제가 발생하는 이유는 무엇입니까?발생하는 문제를 해결하려면 다음을 수행하십시오. 1. 필요한 디렉토리 만들기 mkdir $ home/go mkdir -p $ home/go/src/github.com/user 2. 환경 변수 구성프로그램 작성 2025-05-05에 게시되었습니다 -
 버전 5.6.5 이전에 MySQL의 Timestamp 열을 사용하여 current_timestamp를 사용하는 데 제한 사항은 무엇입니까?5.6.5 이전에 mysql 버전의 기본적으로 또는 업데이트 클로즈가있는 타임 스탬프 열의 제한 사항 5.6.5 5.6.5 이전에 mySQL 버전에서 Timestamp Holumn에 전적으로 기본적으로 한 제한 사항이 있었는데, 이는 제한적으로 전혀 ...프로그램 작성 2025-05-05에 게시되었습니다
버전 5.6.5 이전에 MySQL의 Timestamp 열을 사용하여 current_timestamp를 사용하는 데 제한 사항은 무엇입니까?5.6.5 이전에 mysql 버전의 기본적으로 또는 업데이트 클로즈가있는 타임 스탬프 열의 제한 사항 5.6.5 5.6.5 이전에 mySQL 버전에서 Timestamp Holumn에 전적으로 기본적으로 한 제한 사항이 있었는데, 이는 제한적으로 전혀 ...프로그램 작성 2025-05-05에 게시되었습니다 -
 자바 스크립트 객체의 키를 알파벳순으로 정렬하는 방법은 무엇입니까?object.keys (...) . .sort () . 정렬 된 속성을 보유 할 새 개체를 만듭니다. 정렬 된 키 어레이를 반복하고 리소셔 함수를 사용하여 원래 객체에서 새 객체에 해당 값과 함께 각 키를 추가합니다. 다음 코드는 프로세...프로그램 작성 2025-05-05에 게시되었습니다
자바 스크립트 객체의 키를 알파벳순으로 정렬하는 방법은 무엇입니까?object.keys (...) . .sort () . 정렬 된 속성을 보유 할 새 개체를 만듭니다. 정렬 된 키 어레이를 반복하고 리소셔 함수를 사용하여 원래 객체에서 새 객체에 해당 값과 함께 각 키를 추가합니다. 다음 코드는 프로세...프로그램 작성 2025-05-05에 게시되었습니다 -
 HTML 서식 태그HTML 서식 요소 **HTML Formatting is a process of formatting text for better look and feel. HTML provides us ability to format text without...프로그램 작성 2025-05-05에 게시되었습니다
HTML 서식 태그HTML 서식 요소 **HTML Formatting is a process of formatting text for better look and feel. HTML provides us ability to format text without...프로그램 작성 2025-05-05에 게시되었습니다 -
 크롬에서 상자 텍스트를 선택하는 방법은 무엇입니까?초기 시도 한 가지 일반적인 접근 방식은 다음과 같습니다. 주) & lt;/옵션 & gt; & lt; 옵션> select .lt {text-align : center; } <option value=""&a...프로그램 작성 2025-05-05에 게시되었습니다
크롬에서 상자 텍스트를 선택하는 방법은 무엇입니까?초기 시도 한 가지 일반적인 접근 방식은 다음과 같습니다. 주) & lt;/옵션 & gt; & lt; 옵션> select .lt {text-align : center; } <option value=""&a...프로그램 작성 2025-05-05에 게시되었습니다 -
 교체 지시문을 사용하여 GO MOD에서 모듈 경로 불일치를 해결하는 방법은 무엇입니까?[ github.com/coreos/coreos/client github.com/coreos/etcd/client.test imports github.com/coreos/etcd/integration에 의해 테스트 된 Echoed 메시지에 의해 입증 된 바와...프로그램 작성 2025-05-05에 게시되었습니다
교체 지시문을 사용하여 GO MOD에서 모듈 경로 불일치를 해결하는 방법은 무엇입니까?[ github.com/coreos/coreos/client github.com/coreos/etcd/client.test imports github.com/coreos/etcd/integration에 의해 테스트 된 Echoed 메시지에 의해 입증 된 바와...프로그램 작성 2025-05-05에 게시되었습니다 -
 `JSON '패키지를 사용하여 이동하는 JSON 어레이를 구문 분석하는 방법은 무엇입니까?JSON 어레이를 Parsing JSON 패키지 문제 : JSON 패키지를 사용하여 어레이를 나타내는 JSON 스트링을 어떻게 구문 분석 할 수 있습니까? 예 : type JsonType struct { Array []string ...프로그램 작성 2025-05-05에 게시되었습니다
`JSON '패키지를 사용하여 이동하는 JSON 어레이를 구문 분석하는 방법은 무엇입니까?JSON 어레이를 Parsing JSON 패키지 문제 : JSON 패키지를 사용하여 어레이를 나타내는 JSON 스트링을 어떻게 구문 분석 할 수 있습니까? 예 : type JsonType struct { Array []string ...프로그램 작성 2025-05-05에 게시되었습니다 -
 PHP를 사용하여 Blob (이미지)을 MySQL에 올바르게 삽입하는 방법은 무엇입니까?문제 $ sql = "삽입 ImagesTore (imageId, image) 값 ( '$ this- & gt; image_id', 'file_get_contents ($ tmp_image)'; 결과적으로 실제 이...프로그램 작성 2025-05-05에 게시되었습니다
PHP를 사용하여 Blob (이미지)을 MySQL에 올바르게 삽입하는 방법은 무엇입니까?문제 $ sql = "삽입 ImagesTore (imageId, image) 값 ( '$ this- & gt; image_id', 'file_get_contents ($ tmp_image)'; 결과적으로 실제 이...프로그램 작성 2025-05-05에 게시되었습니다 -
 PHP \의 기능 재정의 제한을 극복하는 방법은 무엇입니까?return $ a * $ b; } 그러나 PHP 도구 벨트에는 숨겨진 보석이 있습니다. runkit_function_rename () runkit_function_rename ( 'this', 'that'); run...프로그램 작성 2025-05-05에 게시되었습니다
PHP \의 기능 재정의 제한을 극복하는 방법은 무엇입니까?return $ a * $ b; } 그러나 PHP 도구 벨트에는 숨겨진 보석이 있습니다. runkit_function_rename () runkit_function_rename ( 'this', 'that'); run...프로그램 작성 2025-05-05에 게시되었습니다 -
 PHP를 사용하여 XML 파일에서 속성 값을 효율적으로 검색하려면 어떻게해야합니까?옵션> 1 varnum "varnum"을 복원 할 수 있습니다. stumped. 이 기능은 XML 요소의 속성에 대한 액세스를 연관 배열로 제공합니다. $ xml = simplexml_load_file ($ file);...프로그램 작성 2025-05-05에 게시되었습니다
PHP를 사용하여 XML 파일에서 속성 값을 효율적으로 검색하려면 어떻게해야합니까?옵션> 1 varnum "varnum"을 복원 할 수 있습니다. stumped. 이 기능은 XML 요소의 속성에 대한 액세스를 연관 배열로 제공합니다. $ xml = simplexml_load_file ($ file);...프로그램 작성 2025-05-05에 게시되었습니다 -
 MySQL에서 데이터를 피벗하여 그룹을 어떻게 사용할 수 있습니까?select d.data_timestamp, sum (data_id = 1 that data_value else 0 End), 'input_1'로 0 End), sum (data_id = 2 an Els.] d.data_timestamp ...프로그램 작성 2025-05-05에 게시되었습니다
MySQL에서 데이터를 피벗하여 그룹을 어떻게 사용할 수 있습니까?select d.data_timestamp, sum (data_id = 1 that data_value else 0 End), 'input_1'로 0 End), sum (data_id = 2 an Els.] d.data_timestamp ...프로그램 작성 2025-05-05에 게시되었습니다
중국어 공부
- 1 "걷다"를 중국어로 어떻게 말하나요? 走路 중국어 발음, 走路 중국어 학습
- 2 "비행기를 타다"를 중국어로 어떻게 말하나요? 坐飞机 중국어 발음, 坐飞机 중국어 학습
- 3 "기차를 타다"를 중국어로 어떻게 말하나요? 坐火车 중국어 발음, 坐火车 중국어 학습
- 4 "버스를 타다"를 중국어로 어떻게 말하나요? 坐车 중국어 발음, 坐车 중국어 학습
- 5 운전을 중국어로 어떻게 말하나요? 开车 중국어 발음, 开车 중국어 학습
- 6 수영을 중국어로 뭐라고 하나요? 游泳 중국어 발음, 游泳 중국어 학습
- 7 자전거를 타다 중국어로 뭐라고 하나요? 骑自行车 중국어 발음, 骑自行车 중국어 학습
- 8 중국어로 안녕하세요를 어떻게 말해요? 你好중국어 발음, 你好중국어 학습
- 9 감사합니다를 중국어로 어떻게 말하나요? 谢谢중국어 발음, 谢谢중국어 학습
- 10 How to say goodbye in Chinese? 再见Chinese pronunciation, 再见Chinese learning

























