परिचय

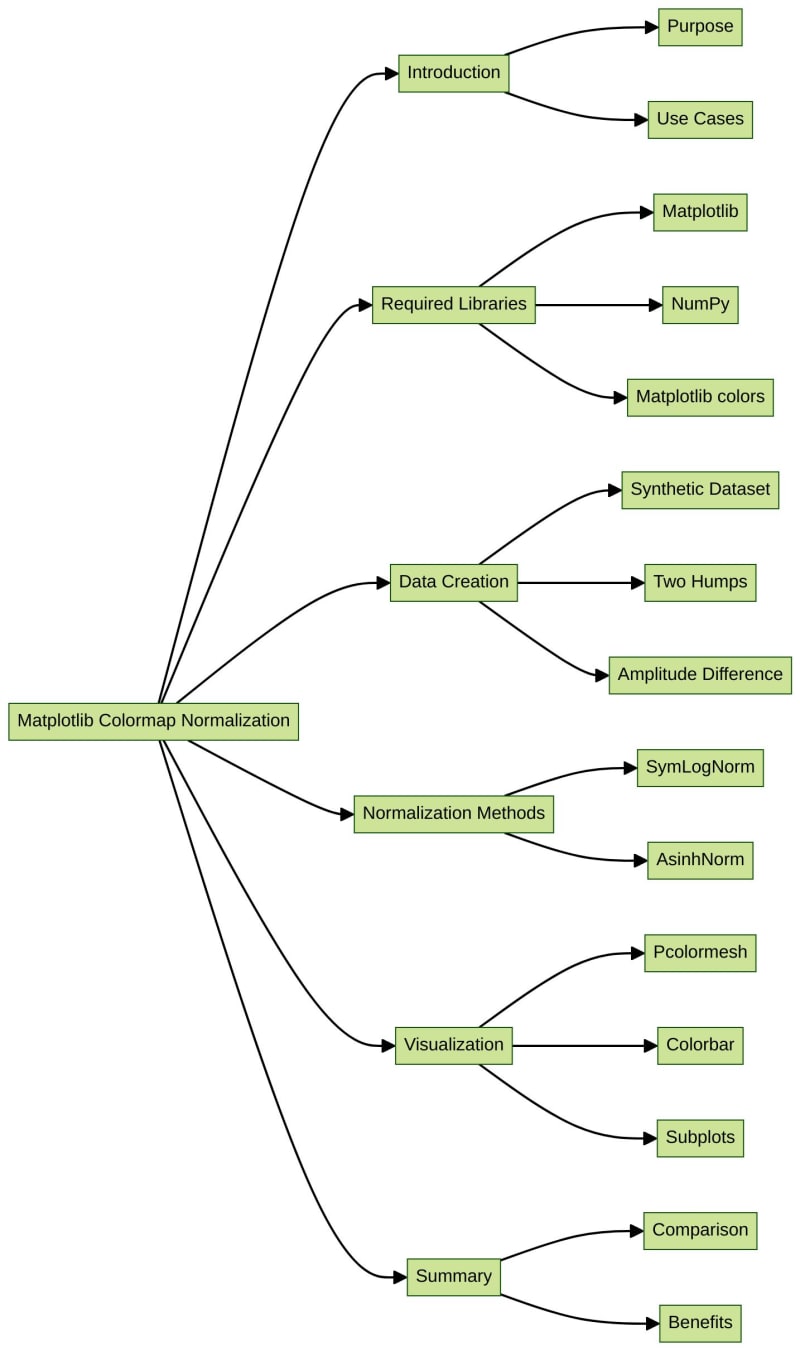
डेटा विज़ुअलाइज़ेशन में, रंग के माध्यम से संख्यात्मक डेटा का प्रतिनिधित्व करने के लिए कलरमैप्स का उपयोग किया जाता है। हालाँकि, कभी-कभी डेटा वितरण अरेखीय हो सकता है, जिससे डेटा के विवरण को समझना मुश्किल हो सकता है। ऐसे मामलों में, डेटा को अधिक सटीक रूप से देखने में मदद करने के लिए नॉनलाइनर तरीकों से डेटा पर कलरमैप को मैप करने के लिए कलरमैप सामान्यीकरण का उपयोग किया जा सकता है। Matplotlib कई सामान्यीकरण विधियाँ प्रदान करता है, जिसमें SymLogNorm और AsainNorm शामिल हैं, जिनका उपयोग कलरमैप्स को सामान्य बनाने के लिए किया जा सकता है। यह प्रयोगशाला प्रदर्शित करेगी कि गैर-रेखीय डेटा पर कलरमैप्स को मैप करने के लिए SymLogNorm और AsinhNorm का उपयोग कैसे करें।

वीएम युक्तियाँ

वीएम स्टार्टअप हो जाने के बाद, अभ्यास के लिए ज्यूपिटर नोटबुक तक पहुंचने के लिए नोटबुक टैब पर स्विच करने के लिए ऊपरी बाएं कोने पर क्लिक करें।

कभी-कभी, ज्यूपिटर नोटबुक की लोडिंग पूरी होने तक आपको कुछ सेकंड इंतजार करना पड़ सकता है। ज्यूपिटर नोटबुक में सीमाओं के कारण संचालन का सत्यापन स्वचालित नहीं किया जा सकता है।

यदि आपको सीखने के दौरान समस्याओं का सामना करना पड़ता है, तो बेझिझक लैबी से पूछें। सत्र के बाद प्रतिक्रिया दें, और हम तुरंत आपकी समस्या का समाधान करेंगे।

आवश्यक पुस्तकालय आयात करें

इस चरण में, हम Matplotlib, NumPy, और Matplotlib रंगों सहित आवश्यक लाइब्रेरी आयात करेंगे।

import matplotlib.pyplot as plt
import numpy as np
import matplotlib.colors as colors

सिंथेटिक डेटा बनाएं

इस चरण में, हम एक सिंथेटिक डेटासेट बनाएंगे जिसमें दो कूबड़ होंगे, एक नकारात्मक और एक सकारात्मक, जिसमें सकारात्मक कूबड़ का आयाम नकारात्मक कूबड़ से आठ गुना अधिक होगा। फिर हम डेटा को विज़ुअलाइज़ करने के लिए SymLogNorm लागू करेंगे।

def rbf(x, y):
    return 1.0 / (1   5 * ((x ** 2)   (y ** 2)))

N = 200
gain = 8
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = rbf(X   0.5, Y   0.5)
Z2 = rbf(X - 0.5, Y - 0.5)
Z = gain * Z1 - Z2

shadeopts = {'cmap': 'PRGn', 'shading': 'gouraud'}
colormap = 'PRGn'
lnrwidth = 0.5

SymLogNorm लागू करें

इस चरण में, हम सिंथेटिक डेटा पर SymLogNorm लागू करेंगे और परिणामों की कल्पना करेंगे।

fig, ax = plt.subplots(2, 1, sharex=True, sharey=True)

pcm = ax[0].pcolormesh(X, Y, Z,
                       norm=colors.SymLogNorm(linthresh=lnrwidth, linscale=1,
                                              vmin=-gain, vmax=gain, base=10),
                       **shadeopts)
fig.colorbar(pcm, ax=ax[0], extend='both')
ax[0].text(-2.5, 1.5, 'symlog')

pcm = ax[1].pcolormesh(X, Y, Z, vmin=-gain, vmax=gain,
                       **shadeopts)
fig.colorbar(pcm, ax=ax[1], extend='both')
ax[1].text(-2.5, 1.5, 'linear')

plt.show()

असिन्हनॉर्म लागू करें

इस चरण में, हम सिंथेटिक डेटा पर असिनहनॉर्म लागू करेंगे और परिणामों की कल्पना करेंगे।

fig, ax = plt.subplots(2, 1, sharex=True, sharey=True)

pcm = ax[0].pcolormesh(X, Y, Z,
                       norm=colors.SymLogNorm(linthresh=lnrwidth, linscale=1,
                                              vmin=-gain, vmax=gain, base=10),
                       **shadeopts)
fig.colorbar(pcm, ax=ax[0], extend='both')
ax[0].text(-2.5, 1.5, 'symlog')

pcm = ax[1].pcolormesh(X, Y, Z,
                       norm=colors.AsinhNorm(linear_width=lnrwidth,
                                             vmin=-gain, vmax=gain),
                       **shadeopts)
fig.colorbar(pcm, ax=ax[1], extend='both')
ax[1].text(-2.5, 1.5, 'asinh')

plt.show()

सारांश

इस प्रयोगशाला में, हमने सीखा कि नॉनलाइनियर डेटा पर कलरमैप्स को मैप करने के लिए SymLogNorm और AsainNorm का उपयोग कैसे करें। इन सामान्यीकरण विधियों को लागू करके, हम डेटा को अधिक सटीक रूप से देख सकते हैं और डेटा के विवरण को अधिक आसानी से समझ सकते हैं।

? अभी अभ्यास करें: मैटप्लोटलिब कलरमैप सामान्यीकरण

और अधिक जानना चाहते हैं?

• ? नवीनतम पायथन स्किल ट्रीज़ सीखें
• ? अधिक पायथन ट्यूटोरियल पढ़ें
• ? हमारे डिस्कॉर्ड में शामिल हों या हमें @WeAreLabEx पर ट्वीट करें