यह अनुभाग पुनरावृत्ति, अनुक्रम और चयन कथनों के लिए बिग ओ निर्धारित करने के कई उदाहरण देता है।

उदाहरण 1

निम्नलिखित लूप के लिए समय जटिलता पर विचार करें:

for (int i = 1; i के = के 5;
}

यह निष्पादित करने के लिए एक निरंतर समय है, सी,

के = के 5;

चूंकि लूप को n बार निष्पादित किया जाता है, लूप के लिए समय जटिलता है

T(n) = (एक स्थिरांक c)*n = O(n).

सैद्धांतिक विश्लेषण एल्गोरिदम के प्रदर्शन की भविष्यवाणी करता है। यह देखने के लिए कि यह एल्गोरिदम कैसा प्रदर्शन करता है, हम n = 1000000, 10000000, 100000000, और 100000000 के लिए निष्पादन समय प्राप्त करने के लिए नीचे दिए गए प्रोग्राम में कोड चलाते हैं।

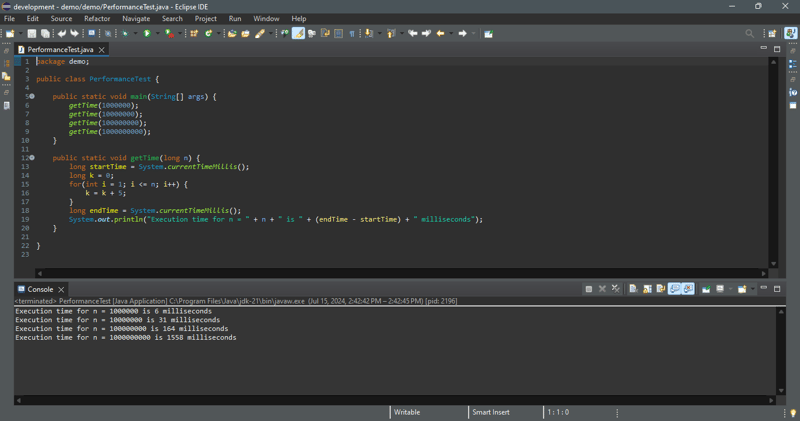
हमारा विश्लेषण इस लूप के लिए एक रैखिक समय जटिलता की भविष्यवाणी करता है। जैसा कि नमूना आउटपुट में दिखाया गया है, जब इनपुट आकार 10 गुना बढ़ जाता है, तो रनटाइम लगभग 10 गुना बढ़ जाता है। निष्पादन भविष्यवाणी की पुष्टि करता है।

उदाहरण 2

निम्नलिखित लूप के लिए समय जटिलता क्या है?

for (int i = 1; i के लिए (int j = 1; j के = के आई जे;
}
}

यह निष्पादित करने के लिए एक निरंतर समय है, सी,

k = k i j;

बाहरी लूप n बार निष्पादित होता है। बाहरी लूप में प्रत्येक पुनरावृत्ति के लिए, आंतरिक लूप को n बार निष्पादित किया जाता है। इस प्रकार, लूप के लिए समय जटिलता है

T(n) = (एक स्थिरांक c)*n*n = O(n^2)

O(n^2) समय जटिलता वाले एक एल्गोरिदम को द्विघात एल्गोरिदम कहा जाता है और यह एक द्विघात विकास दर प्रदर्शित करता है। समस्या का आकार बढ़ने पर द्विघात एल्गोरिथ्म तेजी से बढ़ता है। यदि आप इनपुट आकार को दोगुना कर देते हैं, तो एल्गोरिदम का समय चौगुना हो जाता है। नेस्टेड लूप वाले एल्गोरिदम अक्सर द्विघात होते हैं।

उदाहरण 3

निम्नलिखित लूप पर विचार करें:

for (int i = 1; i के लिए (int j = 1; j के = के आई जे;
}
}

बाहरी लूप n बार निष्पादित होता है। i = 1, 2, c के लिए, आंतरिक लूप को एक बार, दो बार और n बार निष्पादित किया जाता है। इस प्रकार, लूप के लिए समय जटिलता है

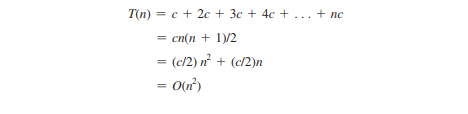
उदाहरण 4

निम्नलिखित लूप पर विचार करें:

for (int i = 1; i के लिए (int j = 1; j के = के आई जे;
}
}

आंतरिक लूप 20 बार निष्पादित होता है, और बाहरी लूप n बार निष्पादित होता है। इसलिए, लूप के लिए समय जटिलता है

T(n) = 20*c*n = O(n)

उदाहरण 5

निम्नलिखित अनुक्रमों पर विचार करें:

for (int j = 1; j के = के 4;
}

for (int i = 1; i के लिए (int j = 1; j के = के आई जे;
}
}

पहला लूप 10 बार निष्पादित होता है, और दूसरा लूप 20 * n बार। इस प्रकार, लूप के लिए समय जटिलता है

टी(एन) = 10*सी 20*सी*एन = ओ(एन)

उदाहरण 6

निम्नलिखित चयन कथन पर विचार करें:

अगर (सूची शामिल है(ई)) {
System.out.println(e);
}
अन्य
(ऑब्जेक्ट टी: सूची) के लिए {
System.out.println(t);
}

मान लीजिए कि सूची में n तत्व हैं। list.contains(e) का निष्पादन समय O(n) है। else क्लॉज में लूप O(n) समय लेता है। इसलिए, पूरे कथन के लिए समय जटिलता है

उदाहरण 7

पूर्णांक n के लिए a^n की गणना पर विचार करें। एक सरल एल्गोरिथ्म n गुना गुणा करेगा, इस प्रकार:

परिणाम = 1;
के लिए (int i = 1; i परिणाम *= ए;

एल्गोरिदम O(n) समय लेता है। व्यापकता की हानि के बिना, n = 2^k मान लें। आप निम्नलिखित योजना का उपयोग करके एल्गोरिदम में सुधार कर सकते हैं:

परिणाम = ए;
के लिए (int i = 1; i परिणाम = परिणाम * परिणाम;

एल्गोरिदम O(logn) समय लेता है। एक मनमाना n के लिए, आप एल्गोरिदम को संशोधित कर सकते हैं और साबित कर सकते हैं कि जटिलता अभी भी O(logn) है।

सरलता के लिए, चूंकि 0(logn) = 0(log2n) = 0(logan), स्थिर आधार हटा दिया गया है।