Programme Java pour supprimer les doublons d'une pile donnée
Dans cet article, nous explorerons deux méthodes pour supprimer les éléments en double d'une pile en Java. Nous comparerons une approche simple avec des boucles imbriquées et une méthode plus efficace utilisant un HashSet. L'objectif est de démontrer comment optimiser la suppression des doublons et d'évaluer les performances de chaque approche.
Énoncé du problème
Écrivez un programme Java pour supprimer l'élément en double de la pile.
Saisir
Stackdata = initData(10L);
Sortir
Unique elements using Naive Approach: [1, 4, 3, 2, 8, 7, 5] Time spent for Naive Approach: 18200 nanoseconds Unique elements using Optimized Approach: [1, 4, 3, 2, 8, 7, 5] Time spent for Optimized Approach: 34800 nanoseconds
Pour supprimer les doublons d'une pile donnée, nous avons 2 approches −
- Approche naïve : créez deux boucles imbriquées pour voir quels éléments sont déjà présents et éviter de les ajouter au retour de la pile de résultats.
- Approche HashSet : utilisez un Set pour stocker des éléments uniques et profitez de sa O(1) complexité pour vérifier si un élément est présent ou non.
Génération et clonage de piles aléatoires
Ci-dessous, le programme Java construit d'abord une pile aléatoire, puis en crée une copie pour une utilisation ultérieure -
private static Stack initData(Long size) {
Stack stack = new Stack ();
Random random = new Random();
int bound = (int) Math.ceil(size * 0.75);
for (int i = 0; i manualCloneStack(Stack stack) {
Stack newStack = new Stack ();
for (Integer item: stack) {
newStack.push(item);
}
return newStack;
}
initData aide à créer une pile avec une taille spécifiée et des éléments aléatoires allant de 1 à 100.
manualCloneStack aide à générer des données en copiant les données d'une autre pile, en les utilisant pour comparer les performances entre les deux idées.
Supprimer les doublons d'une pile donnée à l'aide de l'approche naïve
Voici l'étape pour supprimer les doublons d'une pile donnée en utilisant l'approche naïve −
- Démarrez le minuteur.
- Créez une pile vide pour stocker des éléments uniques.
- Itérer en utilisant la boucle while et continuer jusqu'à ce que la pile d'origine soit vide, pop l'élément supérieur.
- Recherchez les doublons à l'aide de resultStack.contains(element) pour voir si l'élément est déjà dans la pile de résultats.
- Si l'élément n'est pas dans la pile de résultats, ajoutez-le à resultStack.
- Enregistrez l'heure de fin et calculez le temps total passé.
- Retourner le résultat
Exemple
Vous trouverez ci-dessous le programme Java pour supprimer les doublons d'une pile donnée en utilisant l'approche Naïve −
public static Stack idea1(Stack stack) {
long start = System.nanoTime();
Stack resultStack = new Stack ();
while (!stack.isEmpty()) {
int element = stack.pop();
if (!resultStack.contains(element)) {
resultStack.add(element);
}
}
System.out.println("Time spent for idea1 is %d nanosecond".formatted(System.nanoTime() - start));
return resultStack;
}
Pour l'approche Naive, nous utilisons
while (!stack.isEmpty())
resultStack.contains(element)
pour vérifier si l'élément est déjà présent.Supprimer les doublons d'une pile donnée en utilisant une approche optimisée (HashSet)
Voici l'étape pour supprimer les doublons d'une pile donnée en utilisant une approche optimisée −
- Démarrer le minuteur
- Créez un ensemble pour suivre les éléments vus (pour les contrôles de complexité O(1)).
- Créez une pile temporaire pour stocker des éléments uniques.
- Itérer en utilisant la boucle while continuer jusqu'à ce que la pile soit vide.
- Supprimez l'élément supérieur de la pile.
- Pour vérifier les doublons, nous utiliserons seen.contains(element) pour vérifier si l'élément est déjà dans l'ensemble.
- Si l'élément n'est pas dans l'ensemble, ajoutez-le à la fois à la pile vue et à la pile temporaire.
- Enregistrez l'heure de fin et calculez le temps total passé.
- Renvoie le résultat
Exemple
Vous trouverez ci-dessous le programme Java pour supprimer les doublons d'une pile donnée à l'aide de HashSet −
public static Stackidea2(Stack stack) { long start = System.nanoTime(); Set seen = new HashSet(); Stack tempStack = new Stack(); while (!stack.isEmpty()) { int element = stack.pop(); if (!seen.contains(element)) { seen.add(element); tempStack.push(element); } } System.out.println("Time spent for idea2 is %d nanosecond".formatted(System.nanoTime() - start)); return tempStack; }
Pour une approche optimisée, nous utilisons
Set seen Utiliser les deux approches ensemble
Vous trouverez ci-dessous l'étape pour supprimer les doublons d'une pile donnée en utilisant les deux approches mentionnées ci-dessus -
- Initialisez les données, nous utilisons la méthode initData(Long size) pour créer une pile remplie d'entiers aléatoires.
- Clonez la pile, nous utilisons la méthode cloneStack(Stack stack) pour créer une copie exacte de la pile d'origine.
- Générez la pile initiale avec initData.
- Clonez cette pile en utilisant cloneStack.
- Appliquez l' approche naïve pour supprimer les doublons de la pile d'origine.
- Appliquez l'approche optimisée pour supprimer les doublons de la pile clonée.
- Afficher le temps nécessaire à chaque méthode et les éléments uniques produits par les deux approches
Exemple
Vous trouverez ci-dessous le programme Java qui supprime les éléments en double d'une pile en utilisant les deux approches mentionnées ci-dessus −
import java.util.HashSet;
import java.util.Random;
import java.util.Set;
import java.util.Stack;
public class DuplicateStackElements {
private static Stack initData(Long size) {
Stack stack = new Stack();
Random random = new Random();
int bound = (int) Math.ceil(size * 0.75);
for (int i = 0; i cloneStack(Stack stack) {
Stack newStack = new Stack();
newStack.addAll(stack);
return newStack;
}
public static Stack idea1(Stack stack) {
long start = System.nanoTime();
Stack resultStack = new Stack();
while (!stack.isEmpty()) {
int element = stack.pop();
if (!resultStack.contains(element)) {
resultStack.add(element);
}
}
System.out.printf("Time spent for idea1 is %d nanoseconds%n", System.nanoTime() - start);
return resultStack;
}
public static Stack idea2(Stack stack) {
long start = System.nanoTime();
Set seen = new HashSet();
Stack tempStack = new Stack();
while (!stack.isEmpty()) {
int element = stack.pop();
if (!seen.contains(element)) {
seen.add(element);
tempStack.push(element);
}
}
System.out.printf("Time spent for idea2 is %d nanoseconds%n", System.nanoTime() - start);
return tempStack;
}
public static void main(String[] args) {
Stack data1 = initData(10L);
Stack data2 = cloneStack(data1);
System.out.println("Unique elements using idea1: " idea1(data1));
System.out.println("Unique elements using idea2: " idea2(data2));
}
}
Sortir
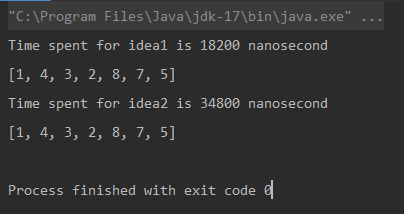
Comparaison
* L'unité de mesure est la nanoseconde.
public static void main(String[] args) {
Stack data1 = initData();
Stack data2 = manualCloneStack(data1);
idea1(data1);
idea2(data2);
}
| Méthode | 100 éléments | 1000 éléments | 10000 éléments |
100 000 éléments |
1 000 000 éléments |
| Idée 1 | 693100 |
4051600 |
19026900 |
114201800 |
1157256000 |
| Idée 2 | 135800 |
681400 |
2717800 |
11489400 |
36456100 |
Comme observé, le temps d'exécution de l'idée 2 est plus court que celui de l'idée 1 car la complexité de l'idée 1 est O(n²), tandis que la complexité de l'idée 2 est O(n). Ainsi, lorsque le nombre de piles augmente, le temps consacré aux calculs augmente également en fonction de celui-ci.
-
 Comment empêcher les soumissions en double après la rafraîchissement du formulaire?Empêcher les soumissions en double avec une manipulation de rafraîchissement dans le développement Web, il est courant d'informer le probl...La programmation Publié le 2025-07-20
Comment empêcher les soumissions en double après la rafraîchissement du formulaire?Empêcher les soumissions en double avec une manipulation de rafraîchissement dans le développement Web, il est courant d'informer le probl...La programmation Publié le 2025-07-20 -
 Comment puis-je lire efficacement un grand fichier dans l'ordre inverse à l'aide de Python?en lisant un fichier dans l'ordre inverse dans python Si vous travaillez avec un grand fichier et que vous devez lire son contenu de la de...La programmation Publié le 2025-07-20
Comment puis-je lire efficacement un grand fichier dans l'ordre inverse à l'aide de Python?en lisant un fichier dans l'ordre inverse dans python Si vous travaillez avec un grand fichier et que vous devez lire son contenu de la de...La programmation Publié le 2025-07-20 -
 Comment puis-je itérer et imprimer des valeurs de manière synchrone à partir de deux tableaux de taille égale en PHP?itération et imprimant de manière synchrone à partir de deux tableaux de même taille lors de la création d'une SelectBox en utilisant deux t...La programmation Publié le 2025-07-20
Comment puis-je itérer et imprimer des valeurs de manière synchrone à partir de deux tableaux de taille égale en PHP?itération et imprimant de manière synchrone à partir de deux tableaux de même taille lors de la création d'une SelectBox en utilisant deux t...La programmation Publié le 2025-07-20 -
 Comment implémenter des événements personnalisés en utilisant le modèle d'observateur en Java?Création d'événements personnalisés dans java Les événements personnalisés sont indispensables dans de nombreux scénarios de programmation, ...La programmation Publié le 2025-07-20
Comment implémenter des événements personnalisés en utilisant le modèle d'observateur en Java?Création d'événements personnalisés dans java Les événements personnalisés sont indispensables dans de nombreux scénarios de programmation, ...La programmation Publié le 2025-07-20 -
 L'erreur du compilateur "USR / bin / ld: ne peut pas trouver -l" solutionErreur rencontrée: "usr / bin / ld: impossible de trouver -l " lorsque -l usr/bin/ld: cannot find -l<nameOfTheLibrary> Ajo...La programmation Publié le 2025-07-20
L'erreur du compilateur "USR / bin / ld: ne peut pas trouver -l" solutionErreur rencontrée: "usr / bin / ld: impossible de trouver -l " lorsque -l usr/bin/ld: cannot find -l<nameOfTheLibrary> Ajo...La programmation Publié le 2025-07-20 -
 Comment détecter efficacement les tableaux vides en PHP?Vérification du vide du tableau en php Un tableau vide peut être déterminé en php via diverses approches. Si le besoin est de vérifier la prés...La programmation Publié le 2025-07-20
Comment détecter efficacement les tableaux vides en PHP?Vérification du vide du tableau en php Un tableau vide peut être déterminé en php via diverses approches. Si le besoin est de vérifier la prés...La programmation Publié le 2025-07-20 -
 Comment ajouter la base de données MySQL à la boîte de dialogue DataSource dans Visual Studio 2012?Ajout de la base de données MySQL à la boîte de dialogue DataSource dans Visual Studio 2012 En travaillant avec Entity Framework et MySQL, l&#...La programmation Publié le 2025-07-20
Comment ajouter la base de données MySQL à la boîte de dialogue DataSource dans Visual Studio 2012?Ajout de la base de données MySQL à la boîte de dialogue DataSource dans Visual Studio 2012 En travaillant avec Entity Framework et MySQL, l&#...La programmation Publié le 2025-07-20 -
 Méthodes d'accès et de gestion des variables d'environnement PythonAccédant aux variables d'environnement en python pour accéder aux variables d'environnement dans Python, utilisez l'objet os.enon...La programmation Publié le 2025-07-20
Méthodes d'accès et de gestion des variables d'environnement PythonAccédant aux variables d'environnement en python pour accéder aux variables d'environnement dans Python, utilisez l'objet os.enon...La programmation Publié le 2025-07-20 -
 Comment résoudre les écarts de chemin du module dans GO Mod en utilisant la directive Remplacer?surmonter la divergence du chemin du module dans go mod Lors de l'utilisation de Go Mod, il est possible de rencontrer un conflit où un pa...La programmation Publié le 2025-07-20
Comment résoudre les écarts de chemin du module dans GO Mod en utilisant la directive Remplacer?surmonter la divergence du chemin du module dans go mod Lors de l'utilisation de Go Mod, il est possible de rencontrer un conflit où un pa...La programmation Publié le 2025-07-20 -
 Comment limiter la plage de défilement d'un élément dans un élément parent de taille dynamique?Implémentation de limites de hauteur CSS pour les éléments de défilement vertical dans une interface interactive, le contrôle du comportement ...La programmation Publié le 2025-07-20
Comment limiter la plage de défilement d'un élément dans un élément parent de taille dynamique?Implémentation de limites de hauteur CSS pour les éléments de défilement vertical dans une interface interactive, le contrôle du comportement ...La programmation Publié le 2025-07-20 -
 PHP Future: adaptation et innovationL'avenir de PHP sera réalisé en s'adaptant aux nouvelles tendances technologiques et en introduisant des fonctionnalités innovantes: 1) s'...La programmation Publié le 2025-07-20
PHP Future: adaptation et innovationL'avenir de PHP sera réalisé en s'adaptant aux nouvelles tendances technologiques et en introduisant des fonctionnalités innovantes: 1) s'...La programmation Publié le 2025-07-20 -
 CSS peut-il localiser les éléments HTML basés sur une valeur d'attribut?ciblant les éléments html avec n'importe quelle valeur d'attribut dans CSS Dans CSS, il est possible de cibler les éléments basés sur ...La programmation Publié le 2025-07-20
CSS peut-il localiser les éléments HTML basés sur une valeur d'attribut?ciblant les éléments html avec n'importe quelle valeur d'attribut dans CSS Dans CSS, il est possible de cibler les éléments basés sur ...La programmation Publié le 2025-07-20 -
 Comment gérer la mémoire tranchée dans la collection d'ordures en langue go?Collection des ordures dans go tranches: une analyse détaillée dans Go, une tranche est un tableau dynamique qui fait référence à un tableau s...La programmation Publié le 2025-07-20
Comment gérer la mémoire tranchée dans la collection d'ordures en langue go?Collection des ordures dans go tranches: une analyse détaillée dans Go, une tranche est un tableau dynamique qui fait référence à un tableau s...La programmation Publié le 2025-07-20 -
 Conseils pour trouver la position d'élément dans Java ArrayRécupération de la position de l'élément dans les tableaux java dans la classe des tableaux de Java, il n'y a pas de méthode directe &...La programmation Publié le 2025-07-20
Conseils pour trouver la position d'élément dans Java ArrayRécupération de la position de l'élément dans les tableaux java dans la classe des tableaux de Java, il n'y a pas de méthode directe &...La programmation Publié le 2025-07-20 -
 Pourquoi Microsoft Visual C ++ ne parvient pas à implémenter correctement l'instanciation du modèle biphasé?Le mystère de l'instanciation du modèle deux phases "Broken" dans Microsoft Visual C Instruction Problème: Les utilisateurs ex...La programmation Publié le 2025-07-20
Pourquoi Microsoft Visual C ++ ne parvient pas à implémenter correctement l'instanciation du modèle biphasé?Le mystère de l'instanciation du modèle deux phases "Broken" dans Microsoft Visual C Instruction Problème: Les utilisateurs ex...La programmation Publié le 2025-07-20
Étudier le chinois
- 1 Comment dit-on « marcher » en chinois ? 走路 Prononciation chinoise, 走路 Apprentissage du chinois
- 2 Comment dit-on « prendre l’avion » en chinois ? 坐飞机 Prononciation chinoise, 坐飞机 Apprentissage du chinois
- 3 Comment dit-on « prendre un train » en chinois ? 坐火车 Prononciation chinoise, 坐火车 Apprentissage du chinois
- 4 Comment dit-on « prendre un bus » en chinois ? 坐车 Prononciation chinoise, 坐车 Apprentissage du chinois
- 5 Comment dire conduire en chinois? 开车 Prononciation chinoise, 开车 Apprentissage du chinois
- 6 Comment dit-on nager en chinois ? 游泳 Prononciation chinoise, 游泳 Apprentissage du chinois
- 7 Comment dit-on faire du vélo en chinois ? 骑自行车 Prononciation chinoise, 骑自行车 Apprentissage du chinois
- 8 Comment dit-on bonjour en chinois ? 你好Prononciation chinoise, 你好Apprentissage du chinois
- 9 Comment dit-on merci en chinois ? 谢谢Prononciation chinoise, 谢谢Apprentissage du chinois
- 10 How to say goodbye in Chinese? 再见Chinese pronunciation, 再见Chinese learning

























