Con frecuencia se ridiculiza JavaScript cuando los desarrolladores encuentran por primera vez este resultado aparentemente desconcertante:

0.1   0.2 == 0.30000000000000004

Los memes sobre el manejo de números por parte de JavaScript están muy extendidos, lo que a menudo lleva a muchos a creer que este comportamiento es exclusivo del lenguaje.

Sin embargo, esta peculiaridad no se limita solo a JavaScript. Es una consecuencia de cómo la mayoría de los lenguajes de programación manejan la aritmética de punto flotante.

Por ejemplo, aquí hay fragmentos de código de Java y Go que producen resultados similares:

Las computadoras de forma nativa solo pueden almacenar números enteros. No entienden fracciones. (¿Cómo lo harán? La única forma en que las computadoras pueden hacer aritmética es encendiendo o apagando algunas luces. La luz puede estar encendida o apagada. ¡No puede estar "medio" encendida!) Necesitan alguna forma de representar números de coma flotante . Dado que esta representación no es perfectamente precisa, la mayoría de las veces, 0,1 0,2 no es igual a 0,3.

Todas las fracciones cuyos denominadores están formados por factores primos de la base del sistema numérico se pueden expresar claramente, mientras que cualquier otra fracción tendría decimales periódicos. Por ejemplo, en el sistema numérico con base 10, fracciones como 1/2, 1/4, 1/5, 1/10 se representan claramente porque los denominadores en cada caso se componen de 2 o 5, los factores primos de 10. Sin embargo, fracciones como 1/3, 1/6, 1/7 tienen decimales recurrentes.

De manera similar, en el sistema binario, fracciones como 1/2, 1/4, 1/8 se expresan claramente, mientras que todas las demás fracciones tienen decimales recurrentes. Cuando realiza aritmética con estos decimales recurrentes, termina con restos que se transfieren cuando convierte la representación binaria de números de la computadora a una representación de base 10 legible por humanos. Esto es lo que conduce a resultados aproximadamente correctos.

Ahora que hemos establecido que este problema no es exclusivo de JavaScript, exploremos cómo se representan y procesan los números de punto flotante para comprender por qué ocurre este comportamiento.

Para comprender cómo se representan y procesan los números de punto flotante, primero tendríamos que comprender el estándar de punto flotante IEEE 754.

El estándar IEEE 754 es una especificación ampliamente utilizada para representar y realizar aritmética en números de punto flotante en sistemas informáticos. Fue creado para garantizar la coherencia al utilizar la aritmética de punto flotante en varias plataformas informáticas. La mayoría de los lenguajes de programación e implementaciones de hardware (CPU, GPU, etc.) se adhieren a este estándar.

Así es como se indica un número en formato IEEE 754:

Aquí s es el bit de signo (0 para positivo, 1 para negativo), M es la mantisa (contiene los dígitos del número) y E es el exponente que determina la escala del número.

No podrás encontrar ningún valor entero para M y E que pueda representar exactamente números como 0,1, 0,2 o 0,3 en este formato. Solo podemos elegir valores para M y E que den el resultado más cercano.

Aquí hay una herramienta que puede utilizar para determinar las notaciones IEEE 754 de números decimales: https://www.h-schmidt.net/FloatConverter/IEEE754.html

Notación IEEE 754 de 0,25:

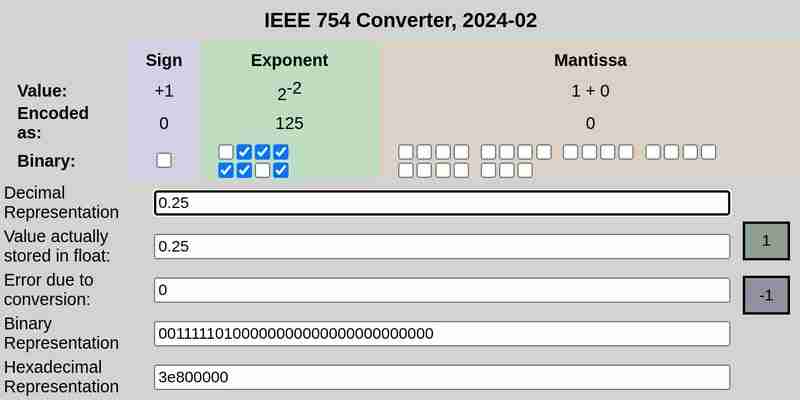
Notación IEEE 754 de 0,1 y 0,2 respectivamente:

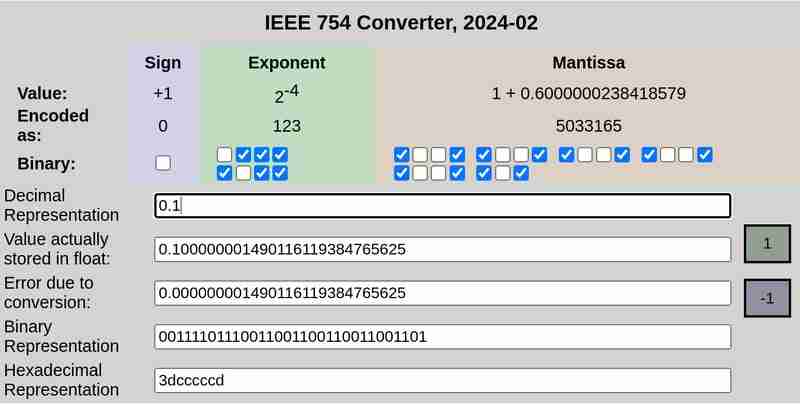
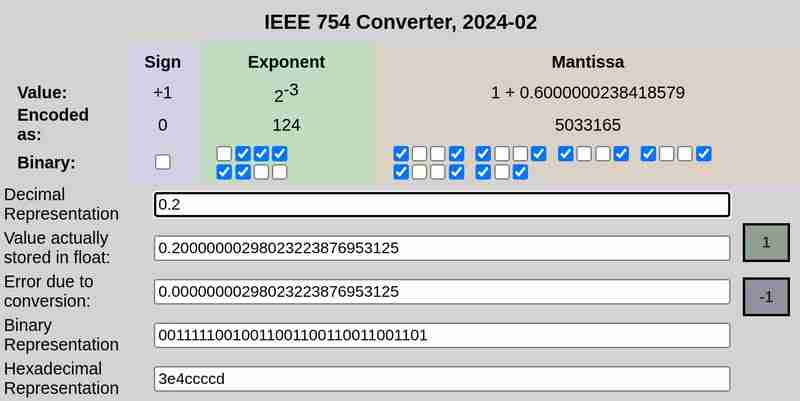
Tenga en cuenta que el error debido a la conversión en el caso de 0.25 fue 0, mientras que 0.1 y 0.2 tuvieron errores distintos de cero.

IEEE 754 define los siguientes formatos para representar números de punto flotante:

• Precisión simple (32 bits): 1 bit para signo, 8 bits para exponente, 23 bits para mantisa

• Doble precisión (64 bits): 1 bit para signo, 11 bits para exponente, 52 bits para mantisa

En aras de la simplicidad, consideremos el formato de precisión simple que utiliza 32 bits.

La representación de 32 bits de 0.1 es:

0 01111011 10011001100110011001101

Aquí el primer bit representa el signo (0 que significa positivo en este caso), los siguientes 8 bits (01111011) representan el exponente y los últimos 23 bits (10011001100110011001101) representan la mantisa.

Esta no es una representación exacta. Representa ≈ 0.100000001490116119384765625

De manera similar, la representación de 32 bits de 0.2 es:

0 01111100 10011001100110011001101

Esta tampoco es una representación exacta. Representa ≈ 0.20000000298023223876953125

Cuando se agrega, esto da como resultado:

0 01111101 11001101010011001100110 

que es ≈ 0.30000001192092896 en representación decimal.

En conclusión, el resultado aparentemente desconcertante de que 0,1 0,2 no arroja 0,3 no es una anomalía específica de JavaScript, sino una consecuencia de las limitaciones de la aritmética de punto flotante en todos los lenguajes de programación. Las raíces de este comportamiento se encuentran en la representación binaria de números, que inherentemente conduce a errores de precisión al manejar ciertas fracciones.