مشكلة المصفوفة الفرعية القصوى وتاريخها

في أواخر السبعينيات، كان عالم الرياضيات السويدي أولف جريناندر يناقش مشكلة: كيف يمكنك تحليل مجموعة ثنائية الأبعاد من بيانات الصور بكفاءة أكبر من القوة الغاشمة؟ كانت أجهزة الكمبيوتر آنذاك بطيئة وكانت الصور كبيرة بالنسبة لذاكرة الوصول العشوائي. لتفاقم الأمور، في أسوأ السيناريوهات، استغرقت القوة الغاشمة وقتًا O(n^6) (تعقيد الوقت الجنسي).

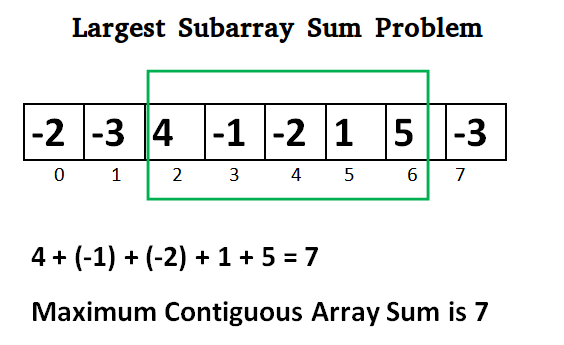
أولاً، قام غريناندير بتبسيط السؤال: بالنظر إلى مجموعة ذات بعد واحد فقط من الأرقام، كيف يمكنك العثور على المصفوفة الفرعية المتجاورة بأكبر قدر من الكفاءة؟

القوة الغاشمة: نهج ساذج مع تعقيد الوقت المكعب

القوة الغاشمة، سيستغرق تحليل مصفوفة أحادية الأبعاد نصف الوقت الذي تستغرقه مصفوفة ثنائية الأبعاد، لذلك O(n^3) لفحص كل مجموعة ممكنة (تعقيد الوقت المكعب).

def max_subarray_brute_force(arr):
    max_sum = arr[0] # assumes arr has a length

    # iterate over all possible subarrays
    for i in range(len(arr)):
        for j in range(i, len(arr)):
            current_sum = 0
            # sum the elements of the subarray arr[i:j 1]
            for k in range(i, j   1):
                current_sum  = arr[k]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

print(max_subarray_brute_force([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

تحسين Grenander's O(n²): خطوة إلى الأمام

قام Grenander بتحسينه إلى حل O(n^2). لم أتمكن من العثور على الكود الخاص به في بحثي، لكن أعتقد أنه تخلص ببساطة من الحلقة الأعمق التي تجمع كل الأرقام بين المؤشرين. بدلاً من ذلك، يمكننا الاحتفاظ بالمجموع الجاري أثناء التكرار على المصفوفة الفرعية، وبالتالي تقليل عدد الحلقات من ثلاث إلى اثنتين.

def max_subarray_optimized(arr):
    max_sum = arr[0]  # assumes arr has a length

    # iterate over all possible starting points of the subarray
    for i in range(len(arr)):
        current_sum = 0
        # sum the elements of the subarray starting from arr[i]
        for j in range(i, len(arr)):
            current_sum  = arr[j]
            # update max_sum if the current sum is greater
            max_sum = max(max_sum, current_sum)

    return max_sum

شاموس فرق تسد: تقسيم المشكلة لـ O(n log n)

أظهر غريناندر المشكلة لعالم الكمبيوتر مايكل شاموس. فكر شاموس في الأمر لليلة واحدة وتوصل إلى طريقة فرق تسد وهي O(n log n).

إنه ذكي جدًا. تتمثل الفكرة في تقسيم المصفوفة إلى نصفين، ثم العثور بشكل متكرر على الحد الأقصى لمجموع المصفوفة الفرعية لكل نصف بالإضافة إلى المصفوفة الفرعية التي تعبر نقطة المنتصف.

def max_crossing_sum(arr, left, mid, right):
    # left of mid
    left_sum = float('-inf')
    current_sum = 0
    for i in range(mid, left - 1, -1):
        current_sum  = arr[i]
        left_sum = max(left_sum, current_sum)

    # right of mid
    right_sum = float('inf')
    current_sum = 0
    for i in range(mid   1, right   1):
        current_sum  = arr[i]
        right_sum = max(right_sum, current_sum)

    # sum of elements on the left and right of mid, which is the maximum sum that crosses the midpoint
    return left_sum   right_sum

def max_subarray_divide_and_conquer(arr, left, right):
    # base case: only one element
    if left == right:
        return arr[left]

    # find the midpoint
    mid = (left   right) // 2

    # recursively find the maximum subarray sum for the left and right halves
    left_sum = max_subarray_divide_and_conquer(arr, left, mid)
    right_sum = max_subarray_divide_and_conquer(arr, mid   1, right)
    cross_sum = max_crossing_sum(arr, left, mid, right)

    # return the maximum of the three possible cases
    return max(left_sum, right_sum, cross_sum)

def max_subarray(arr):
    return max_subarray_divide_and_conquer(arr, 0, len(arr) - 1)


print(max_subarray([-2, -3, 4, -1, -2, 1, 5, -3]), "== 7")

يؤدي هذا إلى تقليل التعقيد الزمني إلى وقت O(nlogn) لأنه أولاً يتم تقسيم المصفوفة إلى نصفين (O(logn)) ثم العثور على الحد الأقصى للصفيف الفرعي المتقاطع يأخذ O(n)

خوارزمية كادان: الحل الأنيق O(n).

نظر الإحصائي جاي كادان إلى الكود وحدد على الفور أن حل شاموس فشل في استخدام قيود التواصل كجزء من الحل.

هذا ما أدركه

-إذا كانت المصفوفة تحتوي على أرقام سالبة فقط، فستكون الإجابة دائمًا هي أكبر رقم في المصفوفة، على افتراض أننا لا نسمح بالمصفوفات الفرعية الفارغة.

-إذا كانت المصفوفة تحتوي على أرقام موجبة فقط، فسيكون الجواب دائمًا هو إضافة المصفوفة بأكملها.

-إذا كان لديك مصفوفة من الأرقام الموجبة والسالبة، فيمكنك اجتياز المصفوفة خطوة بخطوة. إذا كان الرقم الذي تنظر إليه في أي وقت أكبر من مجموع جميع الأرقام التي سبقته، فلا يمكن أن يتضمن الحل أيًا من الأرقام السابقة. وبذلك، تبدأ مبلغًا جديدًا من الرقم الحالي، مع متابعة الحد الأقصى للمبلغ الذي تم مواجهته حتى الآن.

maxSubArray(nums):
    # avoiding type errors or index out of bounds errors
    if nums is None or len(nums) == 0:
        return 0


    max_sum = nums[0]  # max sum can't be smaller than any given element
    curr_sum = 0

    # Kadane's algorithm
    for num in nums:
        curr_sum = max(num, curr_sum   num)
        max_sum = max(curr_sum, max_sum)
    return max_sum

ما أحبه في هذه الخوارزمية هو أنه يمكن تطبيقها على الكثير من المشكلات الأخرى. حاول تكييفه لحل مشاكل LeetCode هذه:

الآحاد والأصفار
الحد الأقصى لمجموع المصفوفة الفرعية الدائرية
الحد الأدنى لحجم مجموع المصفوفة الفرعية
الحد الأقصى لمجموع المصفوفات الفرعية التصاعدية
الحد الأقصى للصفيف الفرعي للمنتج
مجموع المصفوفات الفرعية المستمر
الحد الأقصى للمجموع الفرعي المتناوب (ممتاز)
الحد الأقصى لمجموع المستطيل ليس أكبر من K